5. Análisis de Encuestas Complejas con `srvyr`
0. Objetivos del Práctico
En esta sesión, pondremos en práctica los conceptos de análisis de encuestas complejas utilizando principalmente el paquete srvyr por su sintaxis amigable estilo tidyverse. Al finalizar, podrás:
- Crear un objeto de diseño muestral (
tbl_svy) utilizandosrvyr. - Calcular estimaciones descriptivas ponderadas (medias, proporciones, totales) usando
summarisey las funcionessurvey_*. - Obtener e interpretar medidas de incertidumbre como errores estándar (SE) e intervalos de confianza (IC) para estas estimaciones.
- Realizar análisis descriptivos por subgrupos de manera eficiente usando
group_by. - Visualizar resultados ponderados utilizando
ggplot2después de calcular las estadísticas consrvyr.
1. Preparación y Declaración del Diseño con srvyr
Comenzamos cargando los paquetes necesarios y los datos de CASEN 2022 (igual que en el práctico anterior). Además de tidyverse, haven y survey, ahora cargamos srvyr.
# Cargar paquetes
library(tidyverse)
library(haven)
library(survey)
library(srvyr) # ¡El paquete clave de hoy!
# --- Código para cargar CASEN 2022 (del práctico anterior) ---
# Crear un archivo temporal para la descarga
temp <- tempfile()
# Descargar el archivo .zip que contiene la base de datos SPSS
download.file("https://observatorio.ministeriodesarrollosocial.gob.cl/storage/docs/casen/2022/Base%20de%20datos%20Casen%202022%20SPSS.sav.zip", temp, mode = "wb")
# Leer el archivo .sav
casen <- haven::read_sav(unz(temp, "Base de datos Casen 2022 SPSS.sav"))
# Eliminar el archivo temporal
unlink(temp)
remove(temp)
# (Recodificación de pobreza del práctico anterior, por si acaso)
if (!"pobre_dic" %in% names(casen)) {
casen <- casen %>%
mutate(pobre_dic = ifelse(pobreza %in% c(1, 2), 1, 0))
}
print("Paquetes y datos CASEN 2022 cargados.")
## [1] "Paquetes y datos CASEN 2022 cargados."
# --- Fin del código de carga ---
Ahora, creamos el objeto de diseño tbl_svy usando srvyr::as_survey_design().
# Crear el objeto tbl_svy con srvyr
casen_design_srvyr <- as_survey_design(casen,
ids = varunit, # Variable de conglomerados (UPM)
strata = varstrat, # Variable de estratos
weights = expr ) # Variable de ponderador regional
# Inspeccionar el objeto creado con srvyr
#print(casen_design_srvyr) # Comentado para no alargar el output renderizado
2. Análisis Descriptivo con srvyr
Usaremos el flujo objeto_srvyr %>% summarise(...) para calcular estadísticas descriptivas ponderadas.
Medias Ponderadas
Calculemos la media de edad y escolaridad, pidiendo directamente el Intervalo de Confianza (IC) al 95% (vartype = "ci").
# Calcular medias ponderadas con IC 95%
medias_ci <- casen_design_srvyr %>%
summarise(
edad_media = survey_mean(edad, na.rm = TRUE, vartype = "ci"),
esc_media = survey_mean(esc, na.rm = TRUE, vartype = "ci")
)
print(medias_ci)
## # A tibble: 1 × 6
## edad_media edad_media_low edad_media_upp esc_media esc_media_low esc_media_upp
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 37.2 37.0 37.4 12.0 11.9 12.0
Interpretación: La salida muestra las estimaciones ponderadas y sus intervalos de confianza al 95%.
- Edad: La edad promedio estimada para la población cubierta por CASEN 2022 es 37.2 años. Con un 95% de confianza, la verdadera edad promedio poblacional se encuentra entre 37.0 y 37.4 años.
- Escolaridad: La escolaridad promedio estimada es de 12.0 años. El intervalo de confianza (95%) es muy estrecho, yendo de 11.9 a 12.0 años, lo que indica una alta precisión en esta estimación.
Proporciones Ponderadas
Calcularemos la tasa de pobreza (usando pobre_dic) y la proporción por sexo.
# 1. Proporción de pobreza usando survey_mean en dummy
tasa_pobreza <- casen_design_srvyr %>%
summarise(pobreza_prop = survey_mean(pobre_dic, na.rm = TRUE, vartype = "ci"))
print(tasa_pobreza)
## # A tibble: 1 × 3
## pobreza_prop pobreza_prop_low pobreza_prop_upp
## <dbl> <dbl> <dbl>
## 1 0.0650 0.0622 0.0678
# 2. Proporción por sexo usando group_by + survey_prop
prop_sexo <- casen_design_srvyr %>%
# Usamos as_factor para obtener etiquetas si haven las cargó
mutate(sexo_factor = haven::as_factor(sexo)) %>%
group_by(sexo_factor) %>%
summarise(proporcion = survey_prop(vartype = "ci"))
print(prop_sexo)
## # A tibble: 2 × 4
## sexo_factor proporcion proporcion_low proporcion_upp
## <fct> <dbl> <dbl> <dbl>
## 1 1. Hombre 0.493 0.491 0.496
## 2 2. Mujer 0.507 0.504 0.509
Interpretación:
- Tasa de Pobreza: Se estima que el 6.5% de la población se encuentra en situación de pobreza (extrema o no extrema). El intervalo de confianza del 95% para esta estimación va de 6.2% a 6.8%.
- Distribución por Sexo: La población estimada se distribuye en un 49.3% de hombres (IC 95%: 49.1% - 49.6%) y un 50.7% de mujeres (IC 95%: 50.4% - 50.9%). Los intervalos estrechos reflejan una división muy cercana a la mitad en la población.
Totales Poblacionales Estimados
# Estimar el número total de personas
total_personas <- casen_design_srvyr %>%
summarise(total_pers = survey_total(vartype = "ci"))
print(total_personas)
## # A tibble: 1 × 3
## total_pers total_pers_low total_pers_upp
## <dbl> <dbl> <dbl>
## 1 19878573 19622617. 20134529.
# Estimar el número total de personas en pobreza
total_pobres <- casen_design_srvyr %>%
summarise(total_pob = survey_total(pobre_dic, na.rm = TRUE, vartype = "ci"))
print(total_pobres)
## # A tibble: 1 × 3
## total_pob total_pob_low total_pob_upp
## <dbl> <dbl> <dbl>
## 1 1291824 1234083. 1349565.
Interpretación:
- Población Total: CASEN 2022 estima una población total (cubierta por la encuesta y usando el ponderador regional
expr) de aproximadamente 19.9 millones de personas. El IC 95% sugiere que el valor real está entre 19.6 y 20.1 millones. - Total Personas Pobres: De esa población, se estima que 1,291,824 personas están en situación de pobreza. El IC 95% para este total va desde 1,234,083 hasta 1,349,565 personas.
3. Análisis por Subgrupos (group_by)
Usemos group_by() para calcular estadísticas para diferentes subgrupos.
# Media de ingreso del hogar (ytotcorh) por región
ingreso_x_region <- casen_design_srvyr %>%
mutate(region_factor = haven::as_factor(region)) %>% # Usar etiquetas
filter(pco1== 1) %>% #filtramos por jefe de hogar
group_by(region_factor) %>%
summarise(ingreso_medio_hogar = survey_mean(ytotcorh, na.rm = TRUE, vartype = "se"))
print(ingreso_x_region)
## # A tibble: 16 × 3
## region_factor ingreso_medio_hogar ingreso_medio_hogar_se
## <fct> <dbl> <dbl>
## 1 Región de Tarapacá 1404222. 34297.
## 2 Región de Antofagasta 1679243. 46577.
## 3 Región de Atacama 1338269. 37255.
## 4 Región de Coquimbo 1325239. 39584.
## 5 Región de Valparaíso 1356670. 21570.
## 6 Región del Libertador Gral. Berna… 1289736. 22548.
## 7 Región del Maule 1064411. 15579.
## 8 Región del Biobío 1298370. 24055.
## 9 Región de La Araucanía 1074713. 16027.
## 10 Región de Los Lagos 1278014. 27492.
## 11 Región de Aysén del Gral. Carlos … 1607062. 54578.
## 12 Región de Magallanes y de la Antá… 1680356. 57252.
## 13 Región Metropolitana de Santiago 1965561. 27498.
## 14 Región de Los Ríos 1297774. 29750.
## 15 Región de Arica y Parinacota 1378530. 39979.
## 16 Región de Ñuble 1014487. 18562.
# Tasa de pobreza (proporción de pobre_dic == 1) por zona (urbana/rural)
pobreza_x_zona <- casen_design_srvyr %>%
mutate(zona_factor = haven::as_factor(area)) %>% # Usar etiquetas ('area' es la variable original)
group_by(zona_factor) %>%
summarise(tasa_pobreza = survey_mean(pobre_dic, na.rm = TRUE, vartype = "ci"))
print(pobreza_x_zona)
## # A tibble: 2 × 4
## zona_factor tasa_pobreza tasa_pobreza_low tasa_pobreza_upp
## <fct> <dbl> <dbl> <dbl>
## 1 Urbano 0.0606 0.0576 0.0636
## 2 Rural 0.0994 0.0919 0.107
# Media de escolaridad por sexo
esc_x_sexo <- casen_design_srvyr %>%
mutate(sexo_factor = haven::as_factor(sexo)) %>% # Usar etiquetas
group_by(sexo_factor) %>%
summarise(esc_media = survey_mean(esc, na.rm = TRUE, vartype = "ci"))
print(esc_x_sexo)
## # A tibble: 2 × 4
## sexo_factor esc_media esc_media_low esc_media_upp
## <fct> <dbl> <dbl> <dbl>
## 1 1. Hombre 12.0 12.0 12.1
## 2 2. Mujer 11.9 11.8 11.9
Interpretación y Reflexión:
- Ingreso por Región: La salida
head(ingreso_x_region)muestra el ingreso medio estimado y su error estándar (SE) para las regiones. Vemos diferencias: Antofagasta tiene un ingreso medio estimado más alto ($1,679,243, SE $46,577) que, por ejemplo, Ñuble ($1,014,487, SE $18,562). Errores estándar más pequeños indican mayor precisión en la estimación para esa región específica. - Pobreza por Zona: La tasa de pobreza estimada es notablemente más alta en la zona Rural (9.9%) que en la zona Urbana (6.1%). Crucialmente, los intervalos de confianza no se solapan (Rural: 9.2%-10.7%; Urbana: 5.8%-6.4%). Esto nos da una fuerte evidencia de que la pobreza es significativamente mayor en zonas rurales según esta encuesta.
- Escolaridad por Sexo: La escolaridad media estimada es casi idéntica: 12.0 años para hombres (IC 95%: 12.0 - 12.1) y 11.9 años para mujeres (IC 95%: 11.8 - 11.9). Los intervalos de confianza se solapan, lo que sugiere que la diferencia observada es muy pequeña y probablemente no sea estadísticamente significativa (aunque para confirmarlo necesitaríamos una prueba formal).
4. Visualización de Resultados Ponderados con ggplot2
Recordatorio importante: ggplot2 no aplica automáticamente ponderadores ni calcula errores complejos. Necesita un data frame resumen con las estadísticas ya calculadas correctamente.
El flujo correcto:
- Calcular con
srvyr: Usagroup_byysummarisepara obtener las medias/proporciones y sus ICs/SEs. Guarda esto en un nuevo tibble. - Visualizar con
ggplot2: Usa ese nuevo tibble como input paraggplot.
Ejemplo: Graficar la tasa de pobreza por zona
Reutilizamos el cálculo anterior, asegurándonos de tener el tibble.
# 1. Calcular estadísticas ponderadas con srvyr (ya lo hicimos antes, verificamos)
pobreza_x_zona_data <- casen_design_srvyr %>%
mutate(zona_factor = haven::as_factor(area)) %>%
group_by(zona_factor) %>%
summarise(
tasa_pobreza = survey_mean(pobre_dic, na.rm = TRUE, vartype = "ci")
)
print(pobreza_x_zona_data) # Tibble listo para ggplot
## # A tibble: 2 × 4
## zona_factor tasa_pobreza tasa_pobreza_low tasa_pobreza_upp
## <fct> <dbl> <dbl> <dbl>
## 1 Urbano 0.0606 0.0576 0.0636
## 2 Rural 0.0994 0.0919 0.107
Ahora, graficamos usando pobreza_x_zona_data.
# 2. Crear el gráfico con ggplot2 usando el tibble resumen
ggplot(pobreza_x_zona_data, aes(x = zona_factor, y = tasa_pobreza, fill = zona_factor)) +
geom_col(width = 0.6) + # Gráfico de columnas
geom_errorbar(
aes(ymin = tasa_pobreza_low, ymax = tasa_pobreza_upp), # Usamos los límites del IC
width = 0.2, # Ancho de las barras de error
linewidth = 0.8 # Grosor de la línea
) +
scale_y_continuous(labels = scales::percent_format(accuracy = 1)) + # Eje Y en porcentaje
# Usaremos colores específicos para Urbano/Rural si lo deseamos
# scale_fill_manual(values = c("Urbano" = "lightblue", "Rural" = "darkgreen")) +
scale_fill_viridis_d(option = "D", begin = 0.2, end = 0.7) + # Paleta Viridis (accesible)
labs(
title = "Tasa de Pobreza Estimada por Zona",
subtitle = "Encuesta CASEN 2022 (con IC 95%)",
x = "Zona Geográfica",
y = "Tasa de Pobreza Estimada",
fill = "Zona"
) +
theme_minimal(base_size = 14) +
theme(legend.position = "bottom")
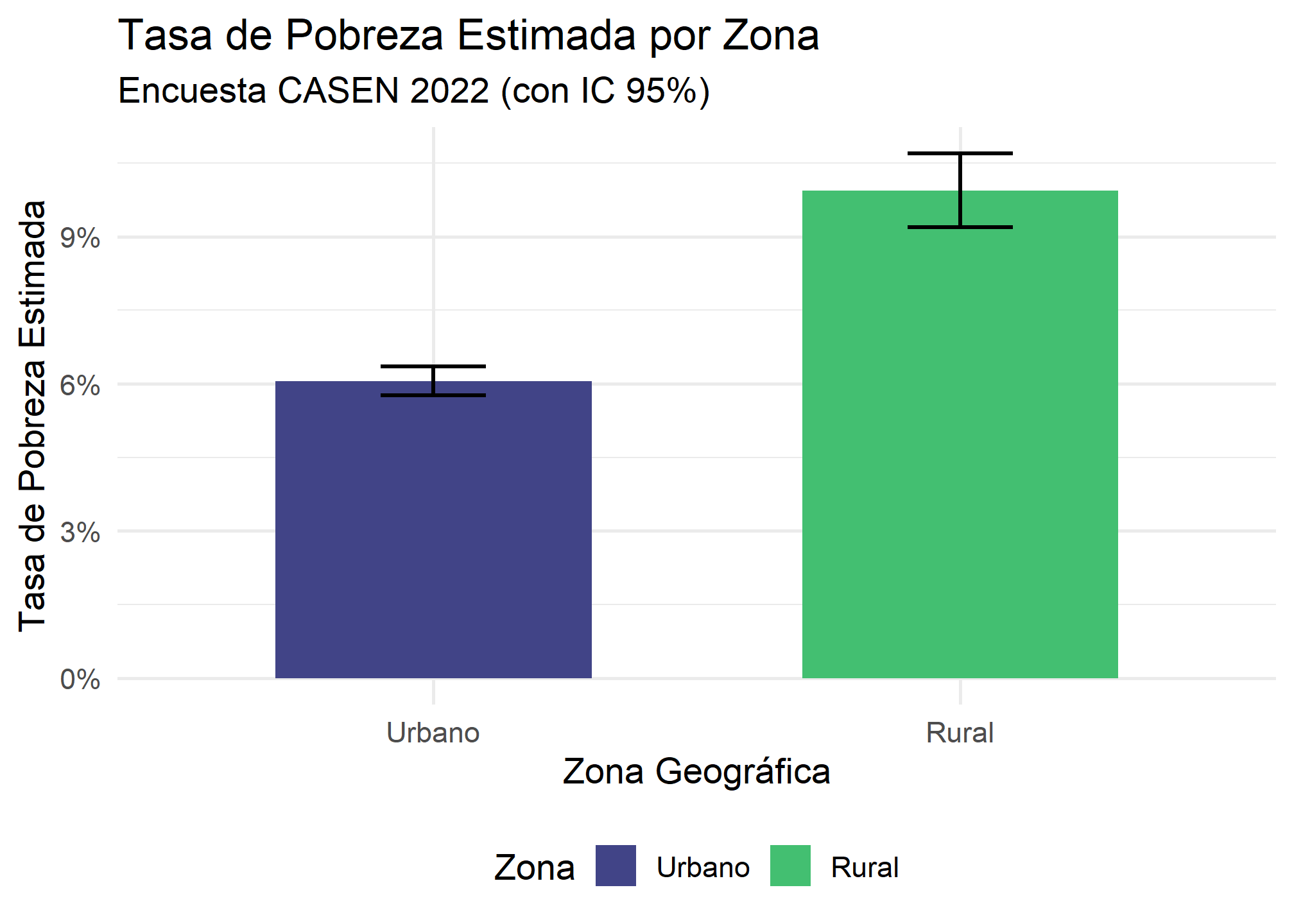
Interpretación del Gráfico: Este gráfico visualiza claramente las estimaciones de pobreza por zona calculadas previamente. Las barras muestran las tasas puntuales (mayor en Rural) y las barras de error (Intervalos de Confianza al 95%) confirman visualmente que la diferencia es significativa, ya que no hay solapamiento entre ellas. El uso de colores distintos ayuda a diferenciar las categorías.
Recuerda: Siempre calcula primero con srvyr/survey, luego visualiza con ggplot2.
5. Conclusión
¡Excelente trabajo! En esta sesión práctica has aprendido a:
- Usar
srvyrpara declarar el diseño muestral de formatidyverse. - Calcular medias, proporciones y totales ponderados usando
summarisey las funcionessurvey_*. - Obtener e interpretar errores estándar e intervalos de confianza que reflejan el diseño complejo.
- Realizar análisis por subgrupos fácilmente con
group_by. - Visualizar correctamente los resultados ponderados usando
ggplot2después de calcular las estadísticas necesarias.
Ahora tienes las herramientas fundamentales para empezar a analizar datos de encuestas complejas como CASEN de manera rigurosa y eficiente en R, incluyendo la capacidad de crear visualizaciones informativas y correctas. ¡El siguiente paso es practicar con diferentes variables y preguntas de investigación!