6. Regresión Lineal Múltiple con Muestras Complejas en R
0. Objetivos del Práctico
En este práctico, aplicaremos la Regresión Lineal Múltiple (RLM) a datos de encuestas complejas usando el paquete survey. Al finalizar, serás capaz de:
- Especificar y ajustar modelos RLM con
survey::svyglm(), incorporando el diseño muestral complejo. - Interpretar correctamente los coeficientes no estandarizados para variables continuas y categóricas (dicotómicas y politómicas), entendiendo el concepto de control estadístico.
- Obtener e interpretar coeficientes estandarizados (Betas) para comparar la magnitud relativa de los efectos.
- Evaluar la significancia estadística de los predictores utilizando los errores estándar y p-valores calculados correctamente por
svyglm. - Realizar e interpretar diagnósticos básicos del modelo (linealidad, homocedasticidad, normalidad de residuos, multicolinealidad) como material complementario.
1. Preparación del Entorno y Datos
Primero, cargamos los paquetes necesarios y preparamos los datos de CASEN 2022.
# Cargar paquetes necesarios. Pacman los instala si no están presentes.
if (!require("pacman")) install.packages("pacman")
pacman::p_load(tidyverse,
haven,
survey,
texreg, # Para tablas de regresión bien formateadas
# jtools, # Removido por ahora, usaremos método manual para estandarizar
car) # Para VIF
# --- Código para cargar CASEN 2022 ---
temp <- tempfile()
download.file("https://observatorio.ministeriodesarrollosocial.gob.cl/storage/docs/casen/2022/Base%20de%20datos%20Casen%202022%20SPSS.sav.zip", temp, mode = "wb")
casen <- haven::read_sav(unz(temp, "Base de datos Casen 2022 SPSS.sav"))
unlink(temp); remove(temp)
print("Datos CASEN 2022 cargados.")
## [1] "Datos CASEN 2022 cargados."
# --- Fin código carga ---
# Seleccionar variables de interés y preparar
casen_model_data <- casen %>%
select(
ytrabajocor, # Ingreso del trabajo (VD)
esc, # Años de escolaridad (VI continua)
edad, # Edad (VI continua)
sexo, # Sexo (VI categórica dicotómica)
region, # Región para crear macrozona (VI categórica politómica)
# Variables de diseño muestral
expr, varstrat, varunit
) %>%
# Crear factor para sexo (1=Hombre, 2=Mujer; R usará Hombre como ref.)
mutate(sexo_factor = factor(sexo, levels = c(1, 2), labels = c("Hombre", "Mujer"))) %>%
# Crear factor para macrozona (Metropolitana como referencia)
mutate(macrozona = case_when(
region %in% c(15, 1, 2, 3, 4) ~ "Norte",
region %in% c(5, 6, 7, 16) ~ "Centro",
region %in% c(8, 9, 14, 10, 11, 12) ~ "Sur",
region == 13 ~ "Metropolitana",
TRUE ~ NA_character_
)) %>%
# Establecer "Metropolitana" como nivel de referencia para el factor
mutate(macrozona = factor(macrozona,
levels = c("Metropolitana", "Norte", "Centro", "Sur"))) %>%
# Filtrar casos con NA en las variables clave del modelo Y LAS VARIABLES DE DISEÑO
# ¡OJO! Esto elimina muchos casos y puede sesgar resultados. Es una simplificación.
filter(complete.cases(ytrabajocor, esc, edad, sexo_factor, macrozona, expr, varstrat, varunit)) %>%
# Filtrar ingresos <= 0
filter(ytrabajocor > 0)
# Verificar dimensiones y estructura final
print(paste("Número de casos completos y con ingreso positivo:", nrow(casen_model_data)))
## [1] "Número de casos completos y con ingreso positivo: 88391"
# glimpse(casen_model_data) # Comentado para brevedad
Ahora, declaramos el diseño muestral complejo usando survey::svydesign().
# Declarar el diseño muestral complejo
casen_design <- svydesign(
ids = ~varunit,
strata = ~varstrat,
weights = ~expr,
data = casen_model_data, # ¡Usamos la base filtrada!
)
print("Objeto de diseño muestral 'casen_design' creado.")
## [1] "Objeto de diseño muestral 'casen_design' creado."
# print(casen_design) # Comentado para brevedad
2. Regresión Lineal Simple con svyglm
Ajustemos un modelo simple de ingresos (ytrabajocor) predichos solo por años de escolaridad (esc).
# Modelo RLS con diseño complejo
modelo_rls_svy <- svyglm(ytrabajocor ~ esc, design = casen_design)
# Resumen del modelo formateado con texreg para HTML
htmlreg(modelo_rls_svy,
custom.coef.names = c("Intercepto", "Años de Escolaridad"),
caption = "Tabla 1: RLS de Ingreso del Trabajo por Escolaridad (CASEN 2022, Diseño Complejo)",
caption.above = TRUE)
| Model 1 | |
|---|---|
| Intercepto | -537674.57*** |
| (24195.72) | |
| Años de Escolaridad | 102894.88*** |
| (2268.17) | |
| Deviance | 72982731141452448.00 |
| Dispersion | 825689909961.00 |
| Num. obs. | 88391 |
| ***p < 0.001; **p < 0.01; *p < 0.05 | |
# --- Para visualización directa en consola (opcional) ---
# Nota: screenreg muestra los resultados directamente en la consola de R.
# screenreg(modelo_rls_svy,
# custom.coef.names = c("Intercepto", "Años de Escolaridad"),
# caption = "Tabla 1: RLS de Ingreso del Trabajo por Escolaridad (CASEN 2022, Diseño Complejo)",
# caption.above = TRUE)
Interpretación (Tabla 1):
- Intercepto (a): El ingreso estimado para una persona con 0 años de escolaridad es de -537,675 pesos. Este valor negativo carece de interpretación práctica en este contexto (ingreso no puede ser negativo y esc=0 es raro para la población trabajadora), pero es el punto donde la línea de regresión cruza el eje Y. Es estadísticamente significativo (p < 0.001).
- Años de Escolaridad (b): Por cada año adicional de escolaridad, se estima que el ingreso del trabajo aumenta en promedio en 102,895 pesos. Este efecto es altamente significativo (p < 0.001), indicando una fuerte relación positiva y lineal entre más años de estudio y mayores ingresos laborales, incluso considerando el diseño complejo.
3. Regresión Lineal Múltiple con svyglm: Control Estadístico
Añadimos edad al modelo para estimar su efecto neto y ver cómo impacta en el coeficiente de esc.
# Modelo RLM con predictores continuos (esc y edad)
modelo_rlm_cont_svy <- svyglm(ytrabajocor ~ esc + edad, design = casen_design)
# Presentar modelos comparados
htmlreg(list(modelo_rls_svy, modelo_rlm_cont_svy),
custom.model.names = c("Modelo 1: RLS (Esc)", "Modelo 2: RLM (Esc + Edad)"),
custom.coef.names = c("Intercepto", "Años de Escolaridad", "Edad"),
caption = "Tabla 2: Comparación RLS y RLM (Continuas)",
caption.above = TRUE)
| Modelo 1: RLS (Esc) | Modelo 2: RLM (Esc + Edad) | |
|---|---|---|
| Intercepto | -537674.57*** | -1151194.26*** |
| (24195.72) | (55376.26) | |
| Años de Escolaridad | 102894.88*** | 115244.37*** |
| (2268.17) | (2773.41) | |
| Edad | 10712.36*** | |
| (626.86) | ||
| Deviance | 72982731141452448.00 | 71314604607645056.00 |
| Dispersion | 825689909961.00 | 806817565421.94 |
| Num. obs. | 88391 | 88391 |
| ***p < 0.001; **p < 0.01; *p < 0.05 | ||
# --- Para visualización directa en consola (opcional) ---
# screenreg(list(modelo_rls_svy, modelo_rlm_cont_svy),
# custom.model.names = c("Modelo 1: RLS (Esc)", "Modelo 2: RLM (Esc + Edad)"),
# custom.coef.names = c("Intercepto", "Años de Escolaridad", "Edad"),
# caption = "Tabla 2: Comparación RLS y RLM (Continuas)",
# caption.above = TRUE)
Interpretación Clave (Tabla 2):
- Coeficiente
esc(Modelo 2): El efecto estimado de la escolaridad aumenta a 115,244 pesos por año adicional, manteniendo laedadconstante. Sigue siendo altamente significativo (p < 0.001). El cambio respecto al Modelo 1 (donde era 102,895) indica que la edad estaba actuando como una variable confusora/supresora; al controlarla, el efecto “puro” de la escolaridad se hace más evidente y fuerte. - Coeficiente
edad(Modelo 2): Por cada año adicional de edad, el ingreso aumenta en promedio en 10,712 pesos, manteniendo la escolaridad constante. Este efecto también es altamente significativo (p < 0.001), sugiriendo que, a igual nivel educativo, la experiencia (aproximada por la edad) también contribuye positivamente al ingreso. - Control Estadístico: El Modelo 2 nos da una imagen más refinada: tanto escolaridad como edad tienen efectos positivos y significativos independientes sobre el ingreso.
4. Incorporando Predictores Categóricos en svyglm
Variable Dicotómica (Sexo)
Añadimos sexo_factor. “Hombre” es la referencia.
# Modelo RLM con predictores continuos y dicotómico (sexo)
modelo_rlm_sexo_svy <- svyglm(ytrabajocor ~ esc + edad + sexo_factor, design = casen_design)
# Tabla comparativa
htmlreg(list(modelo_rlm_cont_svy, modelo_rlm_sexo_svy),
custom.model.names = c("Modelo 2: Esc + Edad", "Modelo 3: Esc + Edad + Sexo"),
custom.coef.names = c("Intercepto", "Años de Escolaridad", "Edad", "Sexo: Mujer (ref. Hombre)"),
caption = "Tabla 3: RLM Añadiendo Sexo",
caption.above = TRUE)
| Modelo 2: Esc + Edad | Modelo 3: Esc + Edad + Sexo | |
|---|---|---|
| Intercepto | -1151194.26*** | -1065119.36*** |
| (55376.26) | (53223.20) | |
| Años de Escolaridad | 115244.37*** | 118138.76*** |
| (2773.41) | (2762.97) | |
| Edad | 10712.36*** | 10503.55*** |
| (626.86) | (617.04) | |
| Sexo: Mujer (ref. Hombre) | -270920.69*** | |
| (8468.38) | ||
| Deviance | 71314604607645056.00 | 69743849066064120.00 |
| Dispersion | 806817565421.94 | 789046827311.51 |
| Num. obs. | 88391 | 88391 |
| ***p < 0.001; **p < 0.01; *p < 0.05 | ||
# --- Para visualización directa en consola (opcional) ---
# screenreg(list(modelo_rlm_cont_svy, modelo_rlm_sexo_svy),
# custom.model.names = c("Modelo 2: Esc + Edad", "Modelo 3: Esc + Edad + Sexo"),
# custom.coef.names = c("Intercepto", "Años de Escolaridad", "Edad", "Sexo: Mujer (ref. Hombre)"),
# caption = "Tabla 3: RLM Añadiendo Sexo",
# caption.above = TRUE)
Interpretación (Tabla 3 - Modelo 3):
- Coeficientes
escyedad: Los efectos de escolaridad (118,139) y edad (10,504) se mantienen positivos y altamente significativos (p < 0.001), ahora controlando también por sexo. Sus magnitudes cambian ligeramente respecto al Modelo 2, lo que indica que el sexo está algo correlacionado con estas variables o sus efectos. - Coeficiente
sexo_factorMujer: El coeficiente es -270,921 (p < 0.001). Esto significa que, en promedio, las mujeres tienen un ingreso del trabajo estimado 270,921 pesos menor que los hombres, incluso cuando tienen la misma cantidad de años de escolaridad y la misma edad. Esta diferencia es estadísticamente muy significativa y representa una brecha de género considerable en los ingresos laborales, independiente de la educación y la edad incluidas en el modelo.
Variable Politómica (Macrozona)
Incluimos macrozona, con “Metropolitana” como referencia.
# Modelo RLM con predictores continuos y politómico (macrozona)
modelo_rlm_macro_svy <- svyglm(ytrabajocor ~ esc + edad + macrozona, design = casen_design)
# Tabla del modelo
htmlreg(modelo_rlm_macro_svy,
custom.coef.names = c("Intercepto", "Años de Escolaridad", "Edad",
"Macrozona: Norte (ref. Metro)",
"Macrozona: Centro (ref. Metro)",
"Macrozona: Sur (ref. Metro)"),
caption = "Tabla 4: RLM con Macrozona",
caption.above = TRUE)
| Model 1 | |
|---|---|
| Intercepto | -1027205.67*** |
| (49868.30) | |
| Años de Escolaridad | 111942.81*** |
| (2563.75) | |
| Edad | 10717.07*** |
| (622.13) | |
| Macrozona: Norte (ref. Metro) | -72809.82*** |
| (15644.48) | |
| Macrozona: Centro (ref. Metro) | -183479.29*** |
| (12435.26) | |
| Macrozona: Sur (ref. Metro) | -156936.01*** |
| (12855.89) | |
| Deviance | 70755152152847824.00 |
| Dispersion | 800488201751.87 |
| Num. obs. | 88391 |
| ***p < 0.001; **p < 0.01; *p < 0.05 | |
# --- Para visualización directa en consola (opcional) ---
# screenreg(modelo_rlm_macro_svy,
# custom.coef.names = c("Intercepto", "Años de Escolaridad", "Edad",
# "Macrozona: Norte (ref. Metro)",
# "Macrozona: Centro (ref. Metro)",
# "Macrozona: Sur (ref. Metro)"),
# caption = "Tabla 4: RLM con Macrozona",
# caption.above = TRUE)
Interpretación (Tabla 4):
- Coeficientes
escyedad: Los efectos de escolaridad (111,943) y edad (10,717) siguen siendo positivos y significativos (p < 0.001), ahora controlando por macrozona geográfica. - Macrozona Norte: El coeficiente es -72,810 (p < 0.001). En promedio, las personas en la Macrozona Norte tienen ingresos estimados 72,810 pesos menores que las de la Región Metropolitana, controlando por escolaridad y edad. La diferencia es significativa.
- Macrozona Centro: Coeficiente -183,479 (p < 0.001). Las personas en la Macrozona Centro tienen ingresos estimados 183,479 pesos menores que en la RM, controlando por esc y edad. Diferencia significativa.
- Macrozona Sur: Coeficiente -156,936 (p < 0.001). Las personas en la Macrozona Sur tienen ingresos estimados 156,936 pesos menores que en la RM, controlando por esc y edad. Diferencia significativa.
- Conclusión: Existen diferencias regionales significativas en los ingresos laborales, incluso después de controlar por diferencias individuales en escolaridad y edad. La Región Metropolitana (referencia) presenta los ingresos estimados más altos.
5. Interpretación Avanzada: Coeficientes Estandarizados (Betas)
Comparamos la “fuerza” relativa de esc y edad en el modelo_rlm_cont_svy (Modelo 2) estandarizando las variables manualmente.
Paso 1: Estandarizar las variables.
casen_model_data_z <- casen_model_data %>%
mutate(
# Estandarizar VD y VIs continuas (media 0, DE 1)
ytrab_z = scale(ytrabajocor)[,1], # scale devuelve una matriz, tomamos la 1ra col
esc_z = scale(esc)[,1],
edad_z = scale(edad)[,1]
)
# Verificar medias y DE
# summary(casen_model_data_z[, c("ytrab_z", "esc_z", "edad_z")]) # Comentado
Paso 2: Re-declarar el diseño y correr svyglm con variables Z.
# RE-Declarar diseño con datos que incluyen variables Z
casen_design_z <- svydesign(
ids = ~varunit, strata = ~varstrat, weights = ~expr,
data = casen_model_data_z, nest = TRUE) # ¡Ojo! Usar la data con Z
# Modelo con variables estandarizadas
modelo_beta_svy <- svyglm(ytrab_z ~ esc_z + edad_z, design = casen_design_z)
# Ver los coeficientes BETA
htmlreg(modelo_beta_svy,
custom.coef.names = c("Intercepto (Z)", "Beta Escolaridad (Z)", "Beta Edad (Z)"),
caption = "Tabla 5: RLM con Variables Estandarizadas (Betas)",
caption.above = TRUE)
| Model 1 | |
|---|---|
| Intercepto (Z) | 0.07*** |
| (0.01) | |
| Beta Escolaridad (Z) | 0.55*** |
| (0.01) | |
| Beta Edad (Z) | 0.19*** |
| (0.01) | |
| Deviance | 106830.21 |
| Dispersion | 1.21 |
| Num. obs. | 88391 |
| ***p < 0.001; **p < 0.01; *p < 0.05 | |
# --- Para visualización directa en consola (opcional) ---
# screenreg(modelo_beta_svy,
# custom.coef.names = c("Intercepto (Z)", "Beta Escolaridad (Z)", "Beta Edad (Z)"),
# caption = "Tabla 5: RLM con Variables Estandarizadas (Betas)",
# caption.above = TRUE)
Interpretación (Tabla 5):
- Beta Escolaridad (Z): El coeficiente estandarizado para
esc_zes 0.55 (p < 0.001). Por cada aumento de 1 desviación estándar en escolaridad, el ingreso del trabajo (también en desviaciones estándar) aumenta en promedio 0.55 DE, controlando por edad (en DE). - Beta Edad (Z): El coeficiente estandarizado para
edad_zes 0.19 (p < 0.001). Por cada aumento de 1 desviación estándar en edad, el ingreso del trabajo aumenta en promedio 0.19 DE, controlando por escolaridad (en DE). - Comparación: El valor absoluto del Beta para escolaridad (0.55) es considerablemente mayor que el de edad (0.19). Conclusión: En este modelo, la escolaridad tiene un impacto relativo más fuerte sobre los ingresos del trabajo que la edad, una vez que se controla por la otra variable.
6. Evaluación del Ajuste y Diagnósticos (Material Complementario)
Revisemos visualmente los supuestos del modelo modelo_rlm_sexo_svy (Modelo 3).
Linealidad (Residuos vs. Ajustados)
plot(modelo_rlm_sexo_svy, which = 1)
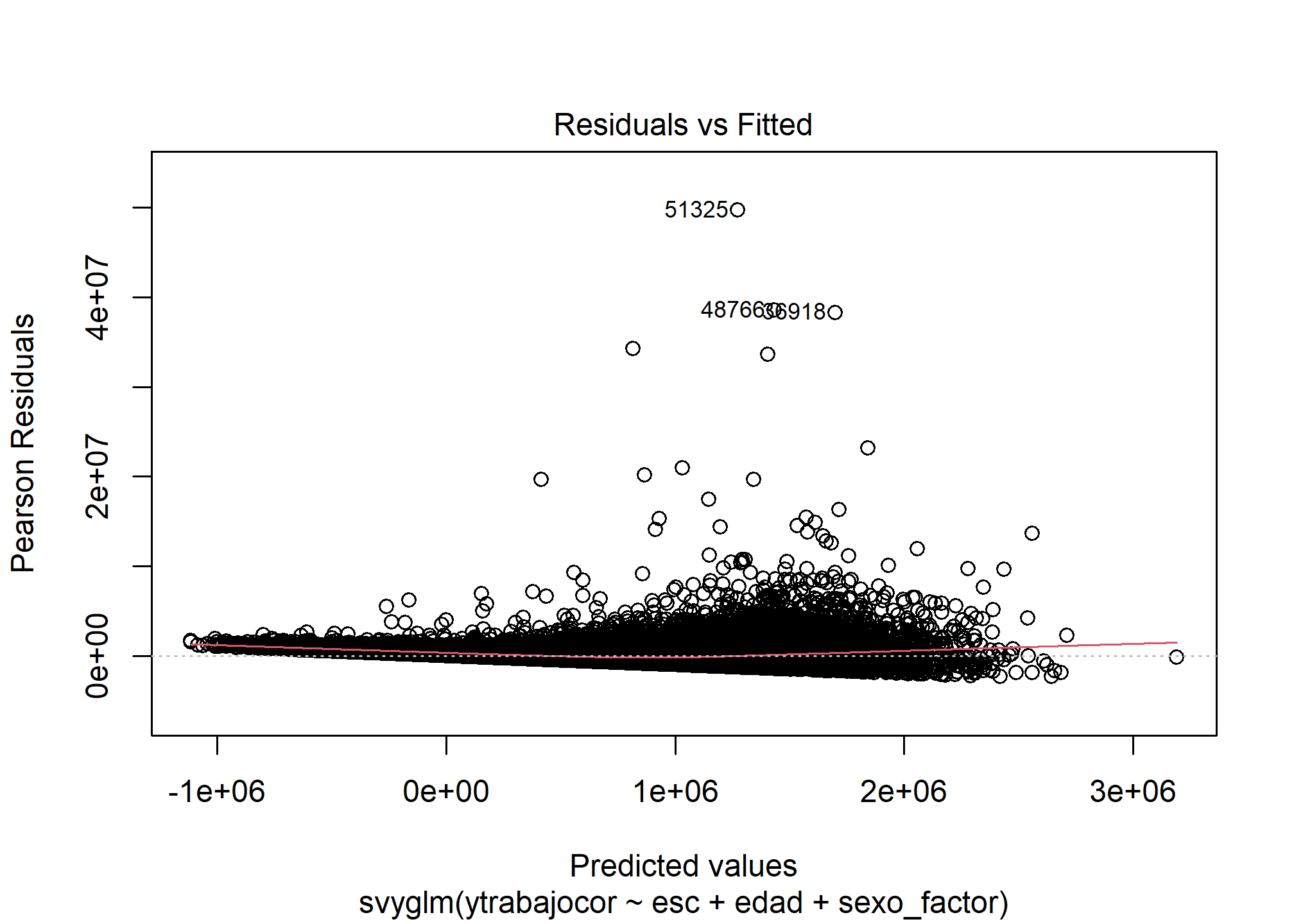
Interpretación: El gráfico de residuos versus valores ajustados muestra una nube de puntos bastante dispersa alrededor de la línea horizontal cero. La línea roja suavizada (LOESS) es relativamente plana, aunque quizás con una ligera tendencia ascendente al final. No se observan patrones curvos fuertes, lo que sugiere que el supuesto de linealidad es razonablemente cumplido, aunque podría haber alguna no linealidad leve no capturada.
Homocedasticidad (Scale-Location)
plot(modelo_rlm_sexo_svy, which = 3)
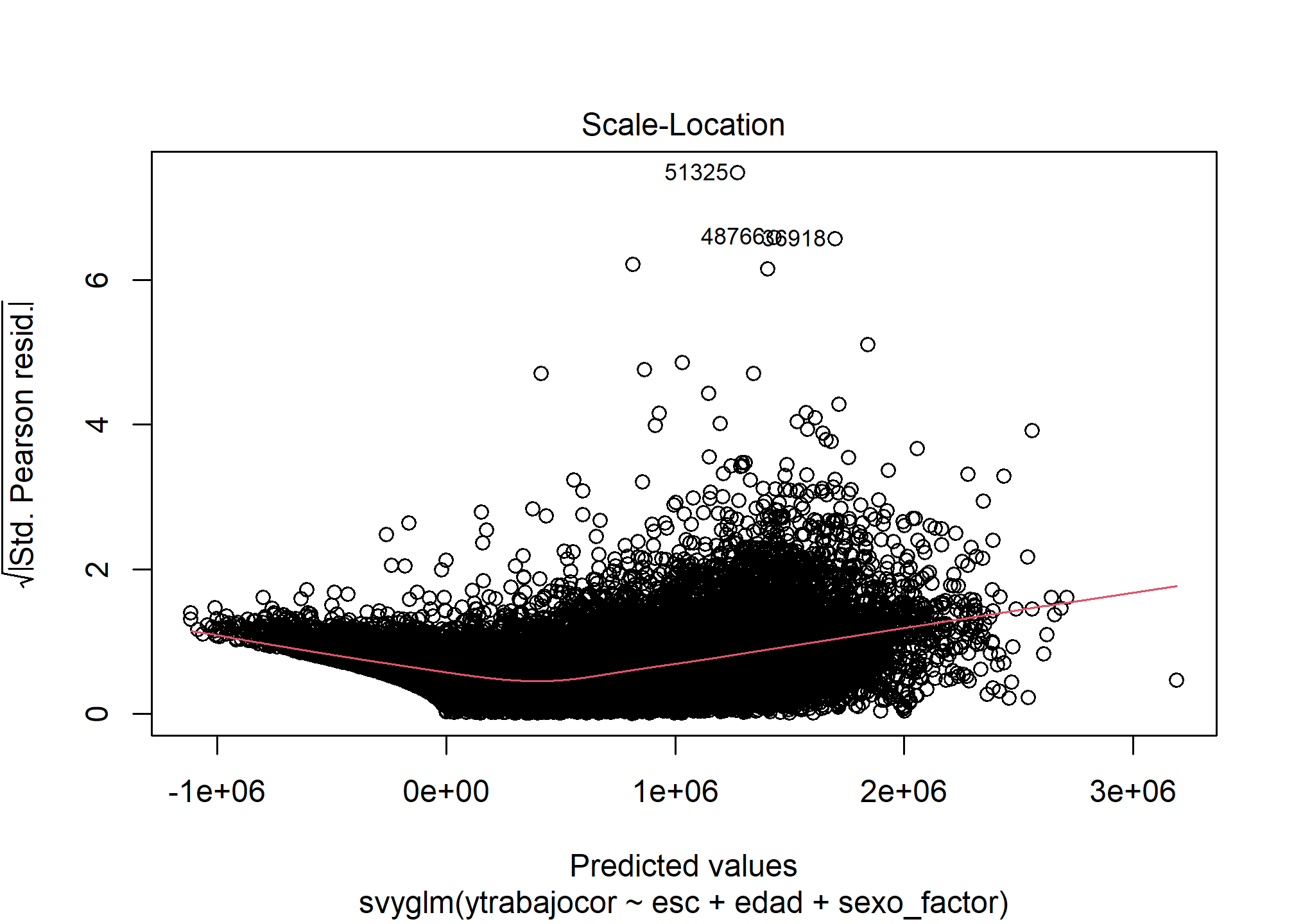
Interpretación: Este gráfico (raíz cuadrada de residuos estandarizados vs. ajustados) muestra una tendencia clara: la línea roja sube y la dispersión de los puntos aumenta a medida que los valores ajustados son mayores. Esto indica heterocedasticidad, es decir, la varianza de los errores no es constante. Los errores son más grandes para predicciones de ingresos más altos. Esto afecta la eficiencia de las estimaciones OLS y la validez de los errores estándar y p-valores calculados por defecto (aunque svyglm ya usa métodos que son algo robustos). En un análisis más avanzado, se podrían usar errores estándar robustos a la heterocedasticidad.
Normalidad de Residuos (Q-Q Plot)
plot(modelo_rlm_sexo_svy, which = 2)
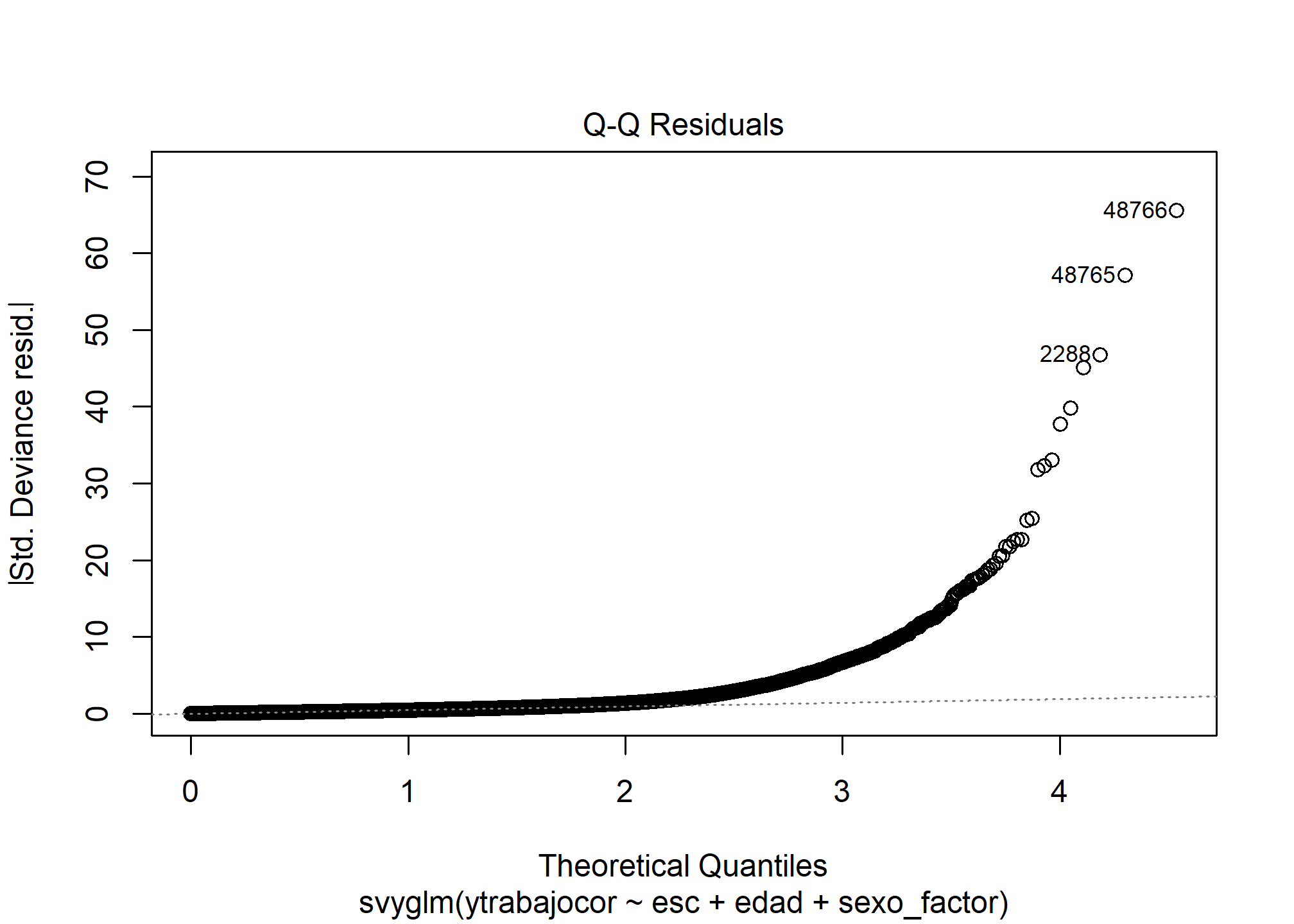
Interpretación: Los puntos se desvían marcadamente de la línea diagonal, especialmente en la cola superior. La distribución de los residuos tiene una cola derecha mucho más larga que una distribución normal (hay residuos positivos mucho más grandes de lo esperado). Esto indica que los residuos no son normales. Dado el gran tamaño muestral (N=88391), la inferencia sobre los coeficientes tiende a ser robusta a esta violación, pero sugiere que el modelo podría mejorarse (quizás transformando la VD, como usando log(ingreso)).
Multicolinealidad (VIF)
Evaluamos si los predictores están demasiado correlacionados entre sí en el Modelo 3.
# Calcular VIF para el modelo con sexo
vif_values_sexo <- car::vif(modelo_rlm_sexo_svy)
print("VIFs para modelo con Esc, Edad, Sexo:")
## [1] "VIFs para modelo con Esc, Edad, Sexo:"
print(vif_values_sexo)
## esc edad sexo_factor
## 3.715365 3.203374 1.395069
Interpretación: Los valores VIF para esc (3.72), edad (3.20) y sexo_factor (1.40) están todos por debajo del umbral problemático (usualmente 5 o 10). Esto indica que la multicolinealidad no es un problema serio en este modelo específico. Podemos interpretar los efectos parciales de cada predictor con relativa confianza.
Casos Influyentes (Residuos vs. Leverage - Mención)
plot(modelo_rlm_sexo_svy, which = 5)
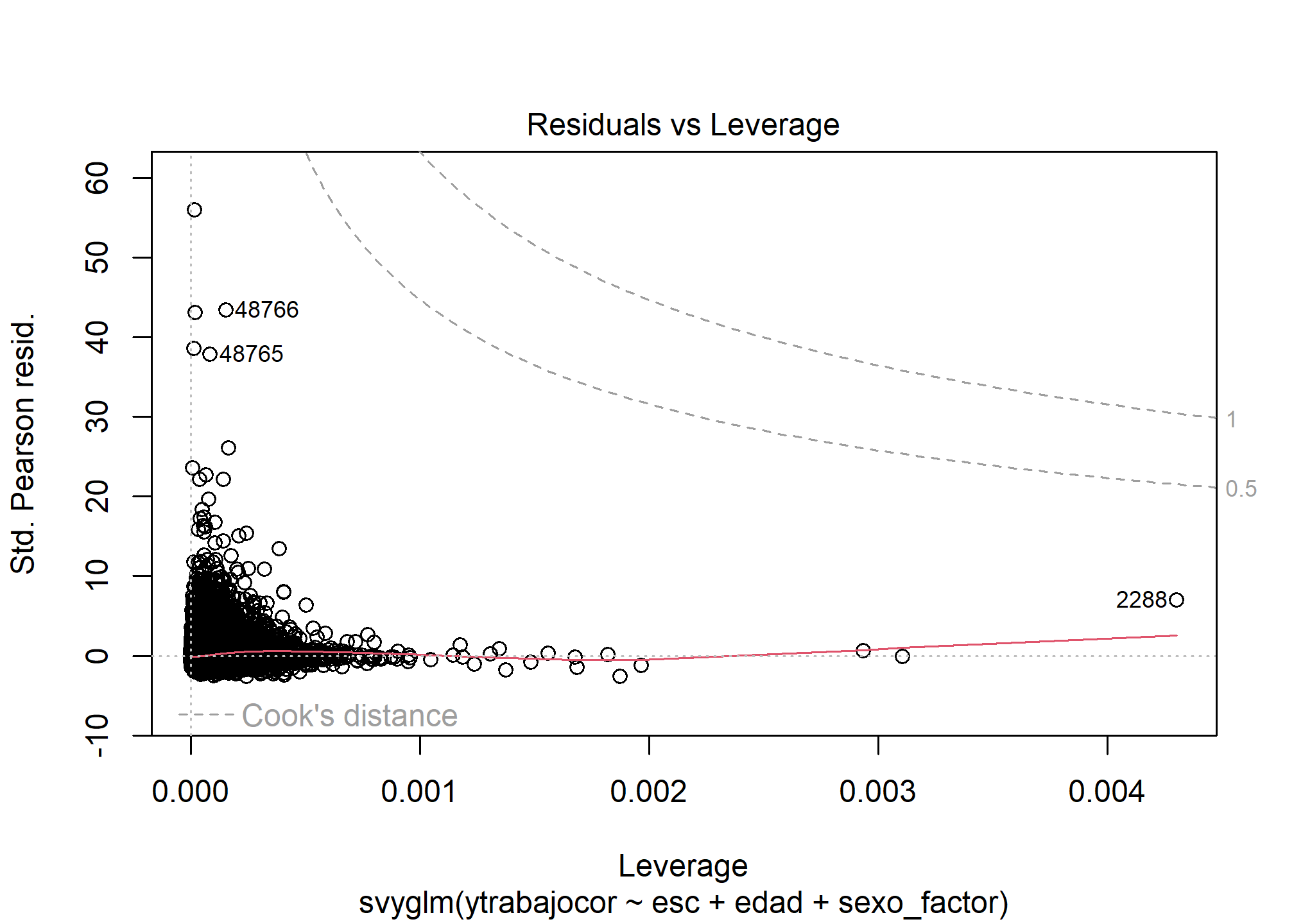
Interpretación: El gráfico muestra varios puntos con residuos estandarizados altos (lejanos a cero en el eje Y), y algunos con leverage moderado (eje X). Los puntos etiquetados (como 48766, 48765) y otros en la esquina superior derecha podrían ser potencialmente influyentes, ya que combinan residuos grandes con cierto leverage. No hay puntos extremadamente alejados en ambas dimensiones simultáneamente, pero valdría la pena investigar los casos con residuos muy grandes en un análisis más profundo.
7. Conclusión
¡Muy bien! En este práctico has avanzado significativamente:
- Ajustaste modelos RLS y RLM usando
svyglm, asegurando que la inferencia estadística respeta el diseño muestral complejo de CASEN. - Practicaste la interpretación de coeficientes parciales para variables continuas y categóricas, entendiendo el control estadístico.
- Aprendiste a calcular e interpretar coeficientes estandarizados (manualmente) para evaluar la importancia relativa de los predictores.
- Realizaste diagnósticos visuales básicos e interpretaste VIFs, identificando heterocedasticidad y no normalidad de residuos como posibles problemas en estos modelos, y confirmando baja multicolinealidad en el modelo con sexo.
Ahora estás mejor equipado para construir, interpretar y evaluar modelos de regresión con datos de encuestas, reconociendo tanto el poder del control estadístico como la importancia de verificar los supuestos y usar las herramientas adecuadas (svyglm) para la inferencia correcta.
Gráfico interactivo de correlación y regresión
A continuación se presenta una herramienta que podrán usar para visualizar de mejor manera como se calcula una correlación o se ajusta una recta de regresión a partir de una nube de puntos.
Para acceder de mejor manera a la aplicación pueden acceder a este enlace: https://gabriel-sotomayor.shinyapps.io/rls_aad/.