7. Análisis Factorial Exploratorio I: Preparación y Supuestos
0. Objetivo del Práctico
El objetivo de este práctico es aprender a realizar los pasos preparatorios cruciales antes de ejecutar un Análisis Factorial Exploratorio (AFE). Nos centraremos en:
- Cargar y gestionar los datos de la encuesta.
- Realizar un análisis descriptivo inicial de las variables.
- Evaluar la adecuación de los datos para el AFE, incluyendo:
- Tratamiento de casos perdidos.
- Identificación y manejo de casos atípicos multivariantes.
- Evaluación de la normalidad univariante y multivariante.
- Análisis de la colinealidad (matriz de correlaciones) y pruebas de factorabilidad (Bartlett y KMO).
1. Carga y Gestión de Datos
Trabajaremos con un extracto de la Encuesta de Desarrollo Humano (EDH) del PNUD, enfocándonos en ítems que miden la percepción sobre las oportunidades que Chile ofrece en diversas áreas.
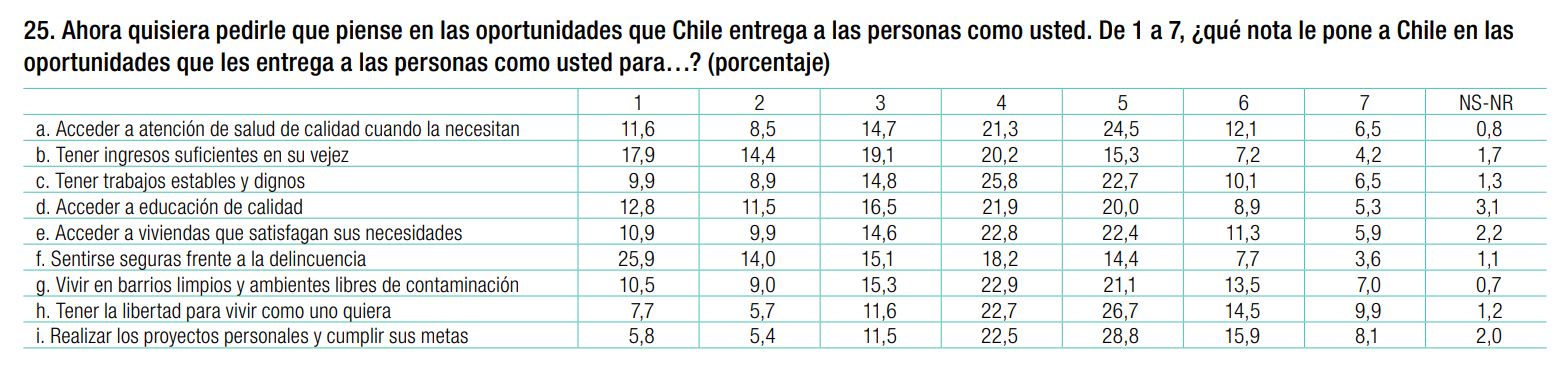
Estos ítems se miden en una escala de 1 (Ninguna oportunidad) a 7 (Muchas oportunidades).
Primero, cargamos los paquetes necesarios y los datos.
# Cargar paquetes
if (!require("pacman")) install.packages("pacman")
pacman::p_load(
tidyverse, # Para manipulación de datos con dplyr
summarytools, # Para resúmenes descriptivos detallados
psych, # Para KMO, Bartlett, y funciones de AFE
MVN) # Para tests de normalidad multivariante
# Cargamos los datos desde la URL
datos <- read.csv("https://raw.githubusercontent.com/Clases-GabrielSotomayor/pruebapagina/master/static/slides/data/EDH_2013_csv.csv") %>%
select(salud = P25a, ingr = P25b, trab = P25c, educ = P25d,
vivi = P25e, segur = P25f, medio = P25g, liber = P25h,
proye = P25i)
glimpse(datos)
## Rows: 1,805
## Columns: 9
## $ salud <int> 5, 3, 1, 7, 3, 6, 3, 5, 6, 6, 4, NA, 5, 5, 1, 4, 4, 3, 5, 6, 2, …
## $ ingr <int> 5, 5, 6, 5, 2, 4, 5, 5, 6, 5, 6, 2, 2, 4, 1, 2, 4, 4, 3, 3, 2, 5…
## $ trab <int> 6, 4, 2, 7, 4, NA, 5, 5, 5, 5, 3, 5, 5, 5, 2, 5, 4, 3, 2, 5, 2, …
## $ educ <int> 6, 4, 4, 7, 1, 4, 6, 6, 6, 4, 4, 5, 1, 6, 1, 5, 5, 1, 4, 4, 2, 5…
## $ vivi <int> 5, 3, 1, 7, 2, 5, 4, 5, 5, 5, 4, NA, 4, 4, 3, 4, 5, 3, 4, 4, 2, …
## $ segur <int> 5, 3, 1, 1, 3, 4, 2, 4, NA, 5, 1, 1, 3, 5, 2, 4, 4, 1, 5, 2, 2, …
## $ medio <int> 7, 4, 4, 7, 1, 5, 4, 6, 5, 5, 7, 5, 1, 5, 5, 6, 4, 3, 5, 2, 2, 6…
## $ liber <int> 7, 4, 4, 7, 2, 5, 5, 6, 6, 4, 7, 6, 5, 5, 3, 6, 5, 2, 4, 6, 2, 5…
## $ proye <int> 7, 4, 2, 7, 3, 5, 6, 5, 5, 5, 2, 7, 4, 6, 6, 6, 5, 3, 4, 6, 2, 6…
Tratamiento de Valores Perdidos
Las variables originales pueden tener códigos para “No sabe” (8) o “No responde” (9). Debemos convertirlos a NA para que R los reconozca como valores perdidos.
# Resumen inicial para ver los valores antes de recodificar
summary(datos)
## salud ingr trab educ
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:3.000 1st Qu.:2.000 1st Qu.:3.000 1st Qu.:3.000
## Median :4.000 Median :3.000 Median :4.000 Median :4.000
## Mean :4.082 Mean :3.433 Mean :4.029 Mean :3.811
## 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:5.000
## Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
## NA's :12 NA's :28 NA's :32 NA's :68
## vivi segur medio liber
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:3.000 1st Qu.:1.000 1st Qu.:3.000 1st Qu.:4.000
## Median :4.000 Median :3.000 Median :4.000 Median :5.000
## Mean :3.993 Mean :3.183 Mean :4.144 Mean :4.476
## 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:6.000
## Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
## NA's :35 NA's :17 NA's :17 NA's :23
## proye
## Min. :1.000
## 1st Qu.:4.000
## Median :5.000
## Mean :4.531
## 3rd Qu.:6.000
## Max. :7.000
## NA's :34
# Recodificar 8 y 9 como NA para todas las variables
datos <- datos %>%
mutate(across(everything(), ~na_if(.x, 9))) %>%
mutate(across(everything(), ~na_if(.x, 8)))
# Verificar que los NAs se hayan asignado (comparar con el summary anterior)
summary(datos)
## salud ingr trab educ
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:3.000 1st Qu.:2.000 1st Qu.:3.000 1st Qu.:3.000
## Median :4.000 Median :3.000 Median :4.000 Median :4.000
## Mean :4.082 Mean :3.433 Mean :4.029 Mean :3.811
## 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:5.000
## Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
## NA's :12 NA's :28 NA's :32 NA's :68
## vivi segur medio liber
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:3.000 1st Qu.:1.000 1st Qu.:3.000 1st Qu.:4.000
## Median :4.000 Median :3.000 Median :4.000 Median :5.000
## Mean :3.993 Mean :3.183 Mean :4.144 Mean :4.476
## 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:6.000
## Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
## NA's :35 NA's :17 NA's :17 NA's :23
## proye
## Min. :1.000
## 1st Qu.:4.000
## Median :5.000
## Mean :4.531
## 3rd Qu.:6.000
## Max. :7.000
## NA's :34
Análisis Descriptivo Inicial
Exploramos las distribuciones, medias y variabilidad de nuestros ítems.
# Usamos dfSummary para un resumen completo
print(dfSummary(datos, headings = FALSE, method = "render", graph.magnif = 0.8))
##
## -------------------------------------------------------------------------------------------
## No Variable Stats / Values Freqs (% of Valid) Graph Valid Missing
## ---- ----------- ----------------------- -------------------- --------- --------- ---------
## 1 salud Mean (sd) : 4.1 (1.8) 1 : 221 (12.3%) II 1793 12
## [integer] min < med < max: 2 : 144 ( 8.0%) I (99.3%) (0.7%)
## 1 < 4 < 7 3 : 255 (14.2%) II
## IQR (CV) : 2 (0.4) 4 : 361 (20.1%) IIII
## 5 : 422 (23.5%) IIII
## 6 : 239 (13.3%) II
## 7 : 151 ( 8.4%) I
##
## 2 ingr Mean (sd) : 3.4 (1.7) 1 : 337 (19.0%) III 1777 28
## [integer] min < med < max: 2 : 240 (13.5%) II (98.4%) (1.6%)
## 1 < 3 < 7 3 : 345 (19.4%) III
## IQR (CV) : 3 (0.5) 4 : 344 (19.4%) III
## 5 : 281 (15.8%) III
## 6 : 143 ( 8.0%) I
## 7 : 87 ( 4.9%)
##
## 3 trab Mean (sd) : 4 (1.7) 1 : 179 (10.1%) II 1773 32
## [integer] min < med < max: 2 : 165 ( 9.3%) I (98.2%) (1.8%)
## 1 < 4 < 7 3 : 267 (15.1%) III
## IQR (CV) : 2 (0.4) 4 : 436 (24.6%) IIII
## 5 : 390 (22.0%) IIII
## 6 : 212 (12.0%) II
## 7 : 124 ( 7.0%) I
##
## 4 educ Mean (sd) : 3.8 (1.7) 1 : 232 (13.4%) II 1737 68
## [integer] min < med < max: 2 : 191 (11.0%) II (96.2%) (3.8%)
## 1 < 4 < 7 3 : 295 (17.0%) III
## IQR (CV) : 2 (0.5) 4 : 376 (21.6%) IIII
## 5 : 345 (19.9%) III
## 6 : 194 (11.2%) II
## 7 : 104 ( 6.0%) I
##
## 5 vivi Mean (sd) : 4 (1.7) 1 : 210 (11.9%) II 1770 35
## [integer] min < med < max: 2 : 164 ( 9.3%) I (98.1%) (1.9%)
## 1 < 4 < 7 3 : 279 (15.8%) III
## IQR (CV) : 2 (0.4) 4 : 370 (20.9%) IIII
## 5 : 390 (22.0%) IIII
## 6 : 237 (13.4%) II
## 7 : 120 ( 6.8%) I
##
## 6 segur Mean (sd) : 3.2 (1.8) 1 : 487 (27.2%) IIIII 1788 17
## [integer] min < med < max: 2 : 224 (12.5%) II (99.1%) (0.9%)
## 1 < 3 < 7 3 : 301 (16.8%) III
## IQR (CV) : 4 (0.6) 4 : 313 (17.5%) III
## 5 : 242 (13.5%) II
## 6 : 156 ( 8.7%) I
## 7 : 65 ( 3.6%)
##
## 7 medio Mean (sd) : 4.1 (1.7) 1 : 191 (10.7%) II 1788 17
## [integer] min < med < max: 2 : 146 ( 8.2%) I (99.1%) (0.9%)
## 1 < 4 < 7 3 : 248 (13.9%) II
## IQR (CV) : 2 (0.4) 4 : 401 (22.4%) IIII
## 5 : 372 (20.8%) IIII
## 6 : 291 (16.3%) III
## 7 : 139 ( 7.8%) I
##
## 8 liber Mean (sd) : 4.5 (1.6) 1 : 141 ( 7.9%) I 1782 23
## [integer] min < med < max: 2 : 91 ( 5.1%) I (98.7%) (1.3%)
## 1 < 5 < 7 3 : 203 (11.4%) II
## IQR (CV) : 2 (0.4) 4 : 383 (21.5%) IIII
## 5 : 452 (25.4%) IIIII
## 6 : 331 (18.6%) III
## 7 : 181 (10.2%) II
##
## 9 proye Mean (sd) : 4.5 (1.6) 1 : 110 ( 6.2%) I 1771 34
## [integer] min < med < max: 2 : 97 ( 5.5%) I (98.1%) (1.9%)
## 1 < 5 < 7 3 : 204 (11.5%) II
## IQR (CV) : 2 (0.3) 4 : 373 (21.1%) IIII
## 5 : 471 (26.6%) IIIII
## 6 : 351 (19.8%) III
## 7 : 165 ( 9.3%) I
## -------------------------------------------------------------------------------------------
Interpretación: La tabla de dfSummary nos muestra:
- Niveles de Medición: Todas nuestras variables son
integer(números enteros). - Valores: Todas van de 1 a 7, como se esperaba.
- Medias y Desviaciones Estándar (sd):
salud: Media 4.1 (DE 1.8)ingr: Media 3.4 (DE 1.7)trab: Media 4.0 (DE 1.7)educ: Media 3.8 (DE 1.7)vivi: Media 4.0 (DE 1.7)segur: Media 3.2 (DE 1.8) - La más baja, junto con ingresos.medio: Media 4.1 (DE 1.7)liber: Media 4.5 (DE 1.6)proye: Media 4.5 (DE 1.6) - Las más altas.
- Missing: Vemos la cantidad y porcentaje de valores perdidos por variable.
educes la que tiene más (3.8%).
En general, las variables no muestran varianzas excesivamente dispares, aunque segur y ingr tienden a tener percepciones más bajas, mientras liber y proye más altas.
2. Comprobación de Supuestos para AFE
Manejo de Casos Perdidos y Creación de Base listwise
Para algunos tests (como el de Mardia para normalidad multivariante) y para simplificar el análisis inicial, crearemos una base de datos eliminando todos los casos que tengan algún valor perdido en cualquiera de los ítems (listwise deletion).
# Guardamos el número de casos originales
n_original <- nrow(datos)
# Creamos la base de datos listwise
datosLW <- na.omit(datos) # na.omit() elimina filas con cualquier NA
# Verificamos las nuevas dimensiones
print(paste("Casos originales:", n_original))
## [1] "Casos originales: 1805"
print(paste("Casos después de listwise deletion (datosLW):", nrow(datosLW)))
## [1] "Casos después de listwise deletion (datosLW): 1654"
print(paste("Casos perdidos por listwise deletion:", n_original - nrow(datosLW)))
## [1] "Casos perdidos por listwise deletion: 151"
Interpretación: Partimos de 1805 casos. Después de eliminar los casos con algún valor perdido en las 9 variables, nos quedamos con 1654 casos. Perdimos 151 casos (aproximadamente 8.4%), lo cual es una cantidad considerable. En un análisis real, investigaríamos si estos casos perdidos tienen algún patrón (no aleatorio) y consideraríamos métodos más sofisticados como la imputación múltiple si la pérdida fuera mayor o sistemática. Para este práctico, continuaremos con datosLW.
Casos Atípicos Multivariantes (Distancia de Mahalanobis)
Identificamos observaciones que son inusuales considerando todas las variables simultáneamente.
# Calcular medias de columnas y matriz de covarianza para datosLW
mean_vars <- colMeans(datosLW) # Usamos datosLW que no tiene NAs
Sx_cov <- cov(datosLW)
# Calcular Distancia de Mahalanobis D^2
D2 <- mahalanobis(datosLW, center = mean_vars, cov = Sx_cov)
# Calcular el p-valor asociado a cada D^2 (chi-cuadrado con df = número de variables)
# df = 9 porque tenemos 9 variables en el análisis
datosLW$p_mahalanobis <- (1 - pchisq(D2, df = ncol(datosLW)))
# Resumen de los p-valores para ver cuántos son atípicos (ej. < 0.001)
summary(datosLW$p_mahalanobis)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.2874 0.7075 0.5941 0.8976 1.0000
print(paste("Número de casos con p_mahalanobis < 0.001:", sum(datosLW$p_mahalanobis < 0.001)))
## [1] "Número de casos con p_mahalanobis < 0.001: 63"
# Eliminar casos atípicos multivariantes (aquellos con p < 0.001)
n_antes_atipicos <- nrow(datosLW)
datosLW_sin_atipicos <- datosLW %>%
filter(p_mahalanobis > 0.001) %>%
select(-p_mahalanobis) # Quitamos la columna del p-valor
print(paste("Casos antes de eliminar atípicos:", n_antes_atipicos))
## [1] "Casos antes de eliminar atípicos: 1654"
print(paste("Casos después de eliminar atípicos (p<0.001):", nrow(datosLW_sin_atipicos)))
## [1] "Casos después de eliminar atípicos (p<0.001): 1591"
print(paste("Casos atípicos multivariantes eliminados:", n_antes_atipicos - nrow(datosLW_sin_atipicos)))
## [1] "Casos atípicos multivariantes eliminados: 63"
# Para el resto del práctico, usaremos datosLW_sin_atipicos renombrado a datosLW
datosLW <- datosLW_sin_atipicos
Interpretación: Se identificaron 63 casos como atípicos multivariantes usando un umbral de p < 0.001 para la distancia de Mahalanobis. Estos casos fueron eliminados, resultando en una base de datos final de 1591 observaciones para los análisis subsecuentes.
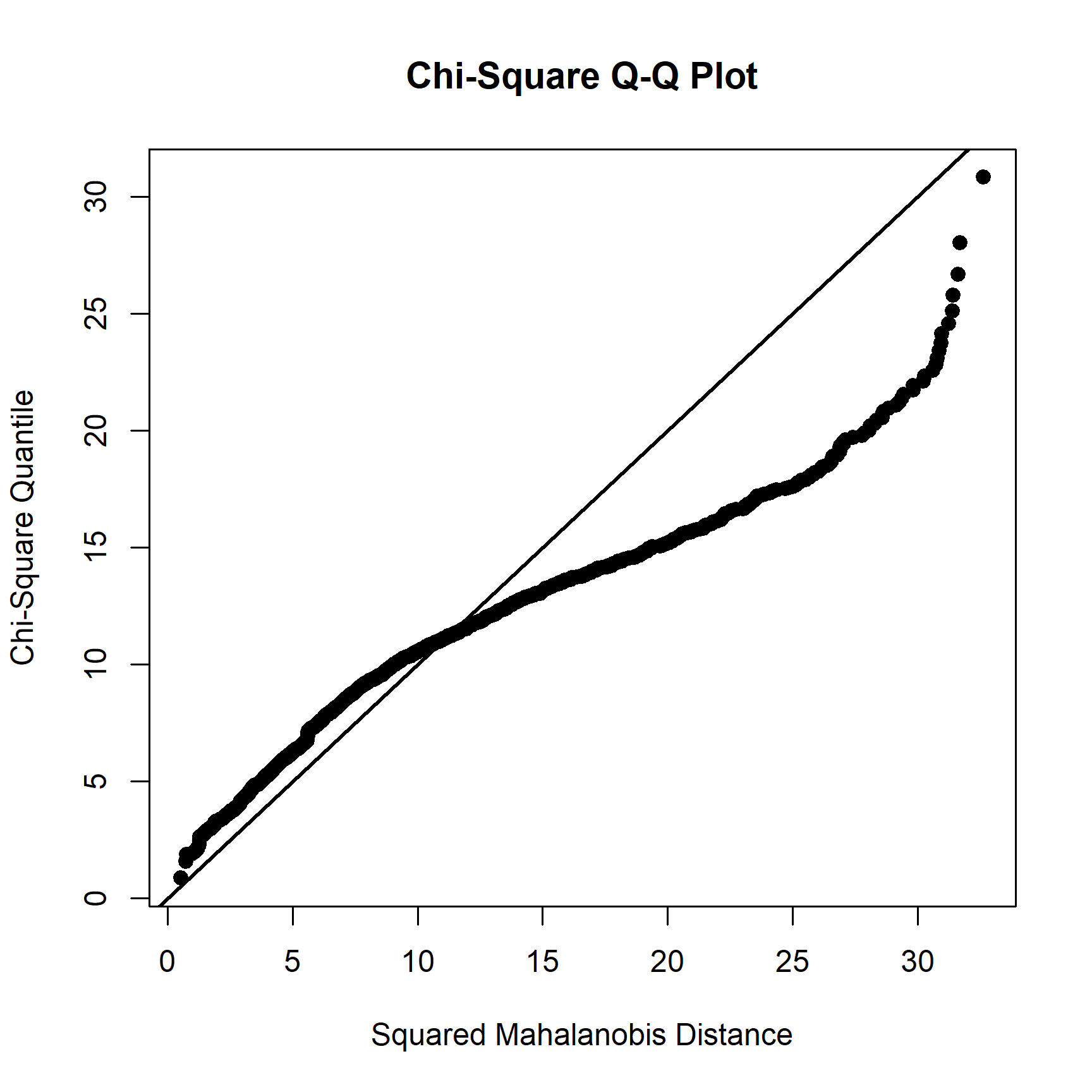
Normalidad Multivariante (Test de Mardia)
Evaluamos si los datos siguen una distribución normal multivariada.
# Test de Mardia usando el paquete MVN
# Usaremos datosLW (que ya no tiene NAs ni atípicos multivariantes)
resultados_mvn <- MVN::mvn(datosLW, mvnTest = "mardia", multivariatePlot = "qq")
print(resultados_mvn$multivariateNormality)
## Test Statistic p value Result
## 1 Mardia Skewness 1729.47785876834 1.34356485870314e-258 NO
## 2 Mardia Kurtosis 33.0432346855492 0 NO
## 3 MVN <NA> <NA> NO
print(resultados_mvn$univariateNormality)
## Test Variable Statistic p value Normality
## 1 Anderson-Darling salud 31.8929 <0.001 NO
## 2 Anderson-Darling ingr 31.6696 <0.001 NO
## 3 Anderson-Darling trab 30.0160 <0.001 NO
## 4 Anderson-Darling educ 29.0099 <0.001 NO
## 5 Anderson-Darling vivi 29.5427 <0.001 NO
## 6 Anderson-Darling segur 45.2613 <0.001 NO
## 7 Anderson-Darling medio 31.0955 <0.001 NO
## 8 Anderson-Darling liber 36.9583 <0.001 NO
## 9 Anderson-Darling proye 37.3868 <0.001 NO
print(resultados_mvn$Descriptives)
## n Mean Std.Dev Median Min Max 25th 75th Skew Kurtosis
## salud 1591 4.055940 1.725871 4 1 7 3 5 -0.22717877 -0.7792271
## ingr 1591 3.462602 1.725416 3 1 7 2 5 0.19055267 -0.8519259
## trab 1591 4.012571 1.630246 4 1 7 3 5 -0.16992697 -0.6457336
## educ 1591 3.817096 1.698644 4 1 7 3 5 -0.05949038 -0.8496713
## vivi 1591 3.971716 1.699376 4 1 7 3 5 -0.15334896 -0.8108244
## segur 1591 3.204903 1.791525 3 1 7 1 5 0.30840123 -0.9764130
## medio 1591 4.082967 1.693689 4 1 7 3 5 -0.23857539 -0.7504117
## liber 1591 4.420490 1.629078 5 1 7 3 6 -0.46962149 -0.3959629
## proye 1591 4.485229 1.566433 5 1 7 4 6 -0.49369218 -0.3003321
Interpretación:
- Normalidad Multivariante (Test de Mardia):
Mardia Skewness(Asimetría): Estadístico = 1729.48, p-valor < 2.2e-16. Resultado: NO normal.Mardia Kurtosis(Curtosis): Estadístico = 33.04, p-valor = 0. Resultado: NO normal.MVN(Combinado): Resultado: NO normal.- Conclusión: Los tests de Mardia indican claramente que los datos no cumplen con el supuesto de normalidad multivariante. El gráfico Q-Q multivariado también mostrará esta desviación de la línea diagonal.
- Normalidad Univariante (Test de Anderson-Darling):
- Para todas y cada una de las 9 variables, el test de Anderson-Darling arroja un p-valor < 0.001, indicando que ninguna de las variables individuales sigue una distribución normal.
- Descriptivos (Asimetría - Skew):
- Los valores de asimetría para todas las variables están entre -0.49 (
proye) y 0.31 (segur). Todos estos valores se encuentran dentro del rango aceptable de\(\pm 2\)(e incluso\(\pm 1\)), lo que sugiere que, aunque no son normales, las distribuciones univariadas no son extremadamente asimétricas. Esto es una buena señal.
- Los valores de asimetría para todas las variables están entre -0.49 (
Implicancias: La falta de normalidad multivariante significa que:
- El Test de Esfericidad de Bartlett (que veremos luego) no será interpretable de forma fiable.
- Si usáramos métodos de extracción factorial que asumen normalidad (como Máxima Verosimilitud - ML), los resultados podrían ser menos precisos. Para este práctico, consideraremos métodos menos sensibles a este supuesto si es necesario más adelante. Por ahora, la moderada asimetría univariada nos permite continuar con cautela.
Colinealidad: Matriz de Correlaciones
El AFE requiere que las variables estén correlacionadas (colinealidad).
# Matriz de Correlaciones de Pearson (dado que las variables son ordinales con 7 categorías
# y la asimetría univariada es moderada, Pearson puede ser una aproximación razonable.
# En un caso más estricto con pocas categorías, se preferirían policóricas).
cor_datos <- cor(datosLW)
print(round(cor_datos, 2)) # Redondeamos para mejor visualización
## salud ingr trab educ vivi segur medio liber proye
## salud 1.00 0.70 0.64 0.68 0.65 0.51 0.58 0.58 0.57
## ingr 0.70 1.00 0.67 0.69 0.66 0.61 0.58 0.53 0.56
## trab 0.64 0.67 1.00 0.76 0.73 0.51 0.61 0.67 0.70
## educ 0.68 0.69 0.76 1.00 0.80 0.60 0.65 0.65 0.67
## vivi 0.65 0.66 0.73 0.80 1.00 0.62 0.65 0.66 0.68
## segur 0.51 0.61 0.51 0.60 0.62 1.00 0.59 0.48 0.47
## medio 0.58 0.58 0.61 0.65 0.65 0.59 1.00 0.72 0.64
## liber 0.58 0.53 0.67 0.65 0.66 0.48 0.72 1.00 0.81
## proye 0.57 0.56 0.70 0.67 0.68 0.47 0.64 0.81 1.00
# Determinante de la matriz de correlaciones
# Un valor cercano a 0 indica multicolinealidad (variables muy relacionadas), lo cual es bueno para AFE.
# Un valor cercano a 1 indicaría variables no correlacionadas.
print(paste("Determinante de la matriz de correlaciones:", det(cor_datos)))
## [1] "Determinante de la matriz de correlaciones: 0.000715319963033099"
Interpretación:
- La matriz muestra correlaciones positivas y generalmente moderadas a altas entre la mayoría de los ítems. Por ejemplo,
educyvivitienen una correlación de 0.80,trabyeducde 0.76. La correlación más baja es entreproyeysegur(0.47). Todas las correlaciones son sustancialmente mayores a 0.30, lo que indica que hay suficiente varianza compartida para un AFE. - El determinante de la matriz de correlaciones es 0.000715, un valor muy cercano a cero. Esto confirma la existencia de alta colinealidad (o multicolinealidad) entre las variables, lo cual es deseable y necesario para el AFE, ya que significa que las variables comparten varianza común que puede ser explicada por factores latentes.
Opcional: Matriz de Correlaciones Policóricas
Dado que las variables son ordinales, una matriz policórica sería teóricamente más adecuada.
# Calcular matriz de correlaciones policóricas
# Nota: puede tardar un poco con muchas variables/casos
matriz_policorica <- polychoric(datosLW)
print(round(matriz_policorica$rho, 2)) # $rho contiene la matriz de correlaciones
## salud ingr trab educ vivi segur medio liber proye
## salud 1.00 0.74 0.67 0.70 0.67 0.54 0.61 0.60 0.59
## ingr 0.74 1.00 0.71 0.73 0.70 0.66 0.62 0.56 0.59
## trab 0.67 0.71 1.00 0.79 0.76 0.55 0.64 0.70 0.73
## educ 0.70 0.73 0.79 1.00 0.83 0.64 0.68 0.68 0.71
## vivi 0.67 0.70 0.76 0.83 1.00 0.66 0.68 0.69 0.71
## segur 0.54 0.66 0.55 0.64 0.66 1.00 0.64 0.52 0.51
## medio 0.61 0.62 0.64 0.68 0.68 0.64 1.00 0.75 0.68
## liber 0.60 0.56 0.70 0.68 0.69 0.52 0.75 1.00 0.84
## proye 0.59 0.59 0.73 0.71 0.71 0.51 0.68 0.84 1.00
Interpretación: Las correlaciones policóricas suelen ser ligeramente más altas que las de Pearson cuando se aplican a datos ordinales, ya que intentan estimar la correlación entre las variables latentes continuas subyacentes. Para nuestros datos, las policóricas confirman el patrón de altas intercorrelaciones. Por ejemplo, educ y vivi es 0.83 (vs 0.80 Pearson).
Factorabilidad de los Datos: Tests de Bartlett y KMO
- Test de Esfericidad de Bartlett:
\(H_0\): La matriz de correlaciones es una matriz identidad (no hay correlación).- Advertencia: Este test asume normalidad multivariante. Dado que nuestros datos no la cumplen, interpretaremos sus resultados con extrema cautela y daremos más peso al KMO.
# Usamos la matriz de correlaciones de Pearson y el N de datosLW
print(cortest.bartlett(cor_datos, n = nrow(datosLW)))
## $chisq
## [1] 11488.26
##
## $p.value
## [1] 0
##
## $df
## [1] 36
Interpretación: El Test de Bartlett arroja un Chi-cuadrado de 11488.26 con 36 grados de libertad, y un p-valor de 0 (muy cercano a cero). Si asumiéramos normalidad, rechazaríamos la hipótesis nula, concluyendo que la matriz de correlaciones es significativamente diferente de una matriz identidad (es decir, hay correlaciones). Dada la falta de normalidad, este resultado es solo indicativo.
- Medida de Adecuación Muestral de Kaiser-Meyer-Olkin (KMO):
- Evalúa si las variables comparten factores comunes. Más robusto a la no normalidad.
# KMO test
KMO(datosLW)
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = datosLW)
## Overall MSA = 0.93
## MSA for each item =
## salud ingr trab educ vivi segur medio liber proye
## 0.95 0.92 0.95 0.94 0.94 0.93 0.94 0.88 0.90
Interpretación:
- Overall MSA (KMO global): 0.93. Este valor se considera “meritorio” o “excelente” (según diferentes guías, >0.8 o >0.9). Indica que los datos son muy adecuados para el análisis factorial. Las variables comparten una cantidad sustancial de varianza común.
- MSA for each item (KMOs individuales): Todos los valores de MSA para los ítems individuales son altos, variando desde 0.88 (
liber) hasta 0.95 (saludytrab). Todos están muy por encima del umbral mínimo aceptable de 0.50 (e incluso del deseable 0.70). Esto significa que cada variable contribuye bien a la estructura factorial común y ninguna necesitaría ser eliminada por baja adecuación muestral.
Conclusión de Supuestos: A pesar de la falta de normalidad multivariante, la moderada asimetría univariada, las altas intercorrelaciones, un determinante cercano a cero y, fundamentalmente, un excelente KMO global e individual, sugieren que los datos son adecuados para proceder con un Análisis Factorial Exploratorio.
3. Siguientes Pasos
Con los datos preparados y los supuestos evaluados favorablemente, los siguientes pasos en un AFE (que se verán en la próxima sesión/práctico) serían:
- Elegir un método de extracción de factores.
- Determinar el número de factores a retener.
- Rotar la solución factorial para mejorar la interpretabilidad.
- Interpretar los factores.