8. Análisis Factorial Exploratorio II: Extracción, Rotación e Interpretación

0. Objetivo del Práctico

Este práctico es la continuación del anterior sobre Análisis Factorial Exploratorio (AFE). Nos centraremos en:

  1. Determinar el número de factores a extraer utilizando el gráfico de sedimentación (scree plot) y el análisis paralelo.
  2. Realizar el AFE con diferentes configuraciones (tipo de correlación, método de rotación), imprimiendo y comparando las soluciones.
  3. Interpretar la matriz factorial resultante (sin rotar y rotada), incluyendo la identificación de cargas factoriales significativas.
  4. Visualizar la estructura factorial con un diagrama.
  5. Calcular y explorar las puntuaciones factoriales para su uso en análisis posteriores.

1. Carga y Preparación de Datos (Recap)

Cargamos los paquetes necesarios y preparamos la base de datos PNUD, aplicando los mismos pasos de limpieza (valores perdidos y atípicos) que en el práctico anterior.

# Cargar paquetes
library(psych) # Para AFE (fa, scree, fa.parallel, KMO, etc.)
library(GPArotation) # Para rotaciones, a menudo cargado con psych
library(dplyr) # Para manipulación de datos

# Cargar datos originales
datosog <- read.csv("https://raw.githubusercontent.com/Clases-GabrielSotomayor/pruebapagina/master/static/slides/data/EDH_2013_csv.csv")

# Seleccionar variables, recodificar NAs y omitir filas con algún NA
datoslw <- datosog %>%
  select(cor, salud = P25a, ingr = P25b, trab = P25c,  educ = P25d, 
         vivi = P25e,  segur = P25f, medio = P25g, liber = P25h, 
         proye = P25i) %>%
  mutate(across(everything(), ~na_if(.x, 9))) %>% # NA si es 9
  mutate(across(everything(), ~na_if(.x, 8))) %>% # NA si es 8
  na.omit() # Eliminar filas con NAs

# Tratamiento de casos atípicos multivariantes (del práctico anterior)
mean_vars <- colMeans(datoslw[, -1], na.rm = TRUE) # Excluimos 'cor' (ID)
Sx_cov <- cov(datoslw[, -1], use = "complete.obs") 
D2 <- mahalanobis(datoslw[, -1], center = mean_vars, cov = Sx_cov)
datoslw$p_mahalanobis <- (1 - pchisq(D2, df = (ncol(datoslw)-1) ))

datoslw <- datoslw %>%
  filter(p_mahalanobis > 0.001) %>%
  select(-p_mahalanobis)

# Guardar ID para posible merge posterior y luego eliminarlo de la base para AFE
id_casos <- datoslw$cor # Guardamos el ID
datoslw$cor <- NULL # Eliminamos la columna 'cor' para el AFE

print(paste("Dimensiones de la base de datos final para AFE (datoslw):", 
            nrow(datoslw), "casos y", ncol(datoslw), "variables."))

## [1] "Dimensiones de la base de datos final para AFE (datoslw): 1591 casos y 9 variables."

Nota: Después de la limpieza, nos quedamos con 1591 casos para el análisis.

2. Determinando el Número de Factores

Gráfico de Sedimentación (Scree Plot)

scree(datoslw, factors = TRUE, pc = TRUE)

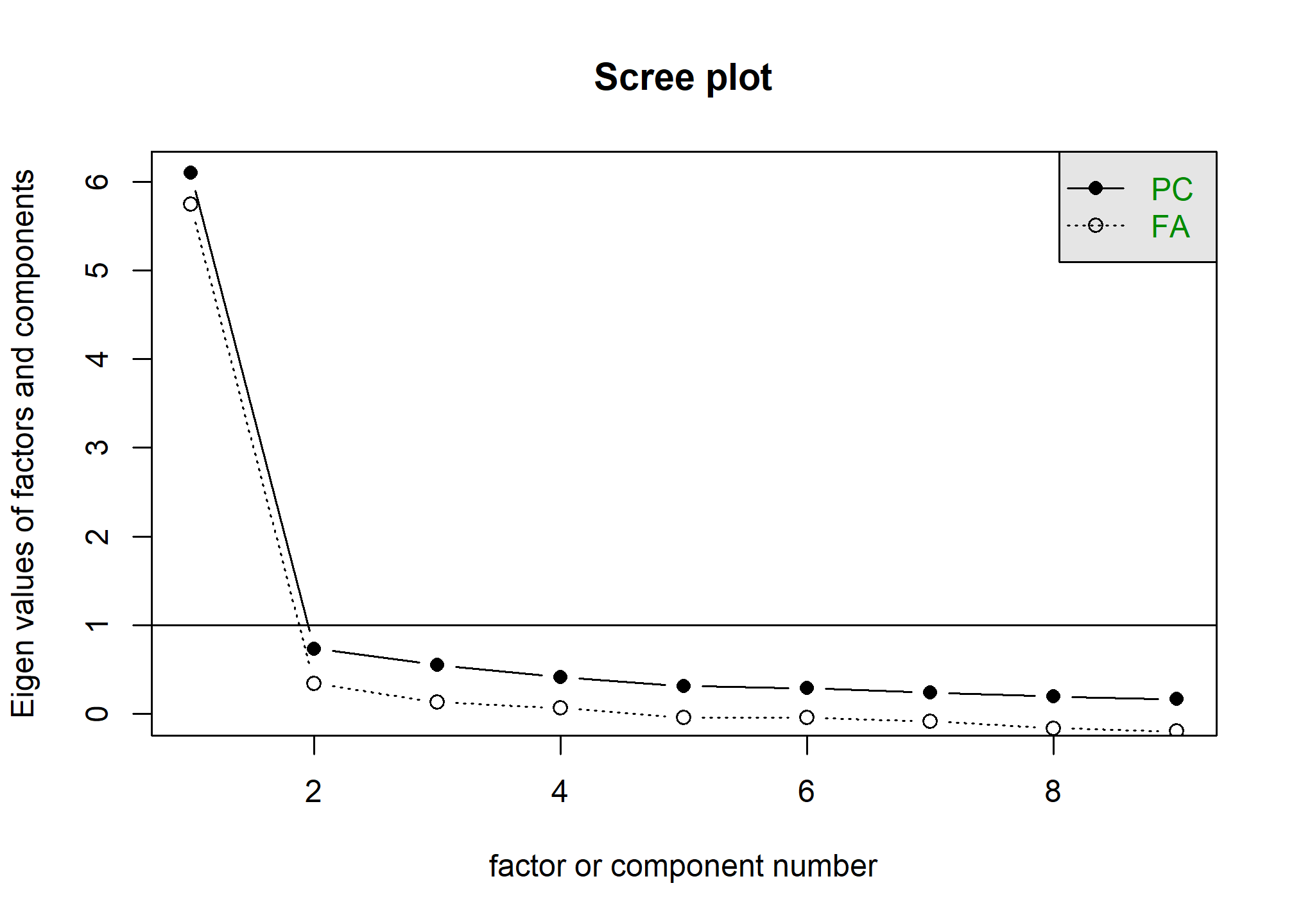Interpretación del Scree Plot: La línea continua (PC - Componentes Principales) muestra una caída muy pronunciada después del primer componente (autovalor cercano a 6), seguido de un “codo” y luego una estabilización con autovalores por debajo de 1. Esto sugeriría un solo componente principal dominante. La línea punteada (FA - Análisis Factorial, basada en la matriz de correlación reducida) también muestra una caída fuerte después del primer factor, aunque los autovalores son menores. El “codo” aquí también es evidente después del primer factor, con los subsiguientes muy cerca del eje. Si nos guiamos solo por el criterio del codo, especialmente para FA, podría sugerirse una solución de 1 o quizás 2 factores. El Criterio de Kaiser (autovalor > 1 para PCA) apuntaría a 1 solo componente.

Análisis Paralelo

set.seed(231) # Para reproducibilidad
analisis_paralelo <- fa.parallel(datoslw, fa = "fa") 


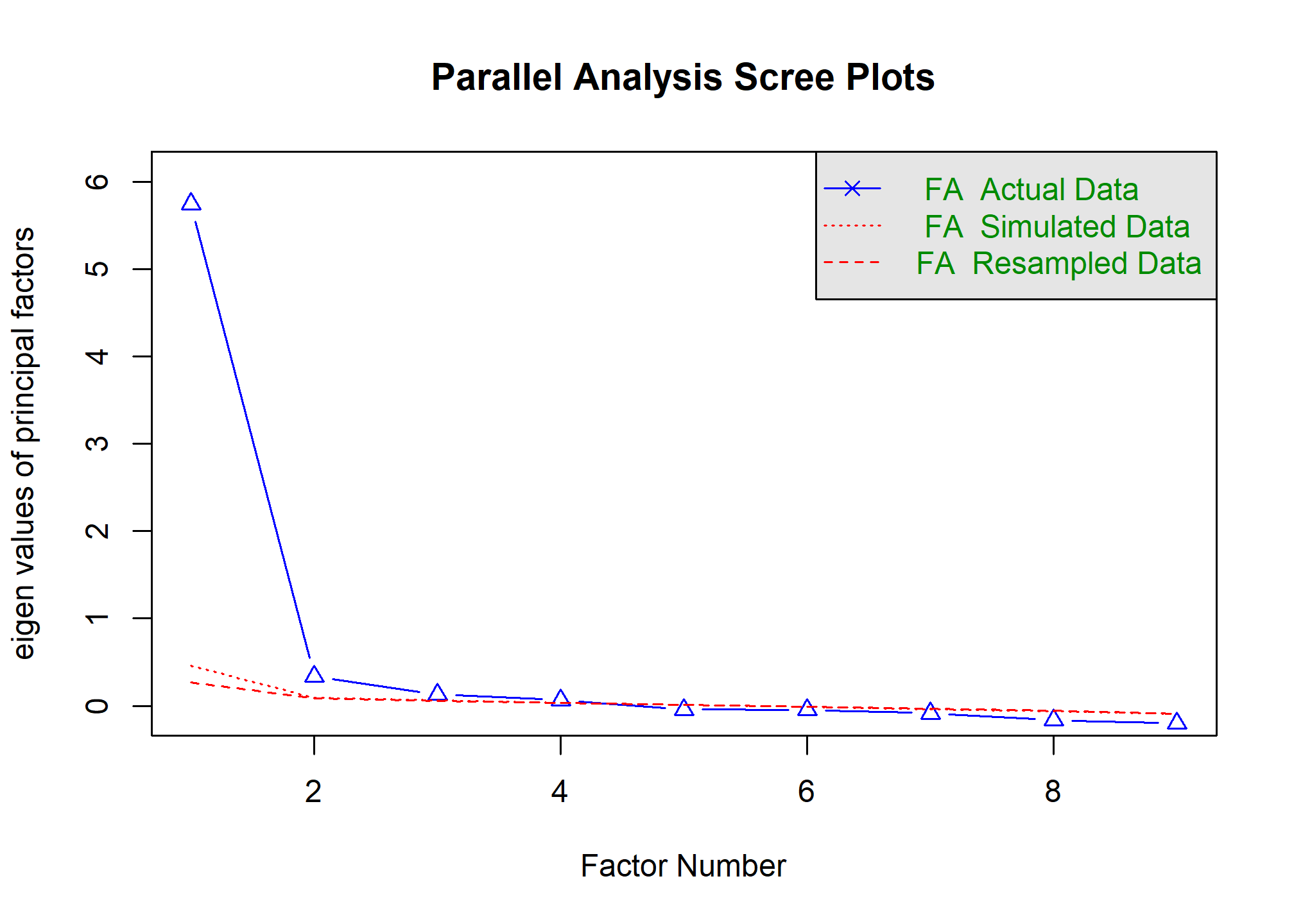
## Parallel analysis suggests that the number of factors =  4  and the number of components =  NA

#print(analisis_paralelo$fa.values) # Comentado, ya que el gráfico es más informativo y el texto lo resume

Interpretación del Análisis Paralelo: El output textual clave es: Parallel analysis suggests that the number of factors = 4. Observando el gráfico:

  • El primer autovalor de los datos reales (línea azul FA Actual Data) es muy alto (5.75).
  • Los autovalores segundo, tercero y cuarto de los datos reales (0.34, 0.13, 0.06 respectivamente) se mantienen por encima de las líneas rojas punteada (FA Simulated Data - promedio de datos aleatorios) y discontinua (FA Resampled Data).
  • A partir del quinto factor, los autovalores de los datos reales caen por debajo de los esperados por azar. Conclusión: El análisis paralelo, un criterio más robusto, sugiere retener 4 factores. Procederemos con esta recomendación.

3. Análisis Factorial Exploratorio (AFE)

Con 4 factores a extraer y sabiendo que nuestras variables son ordinales, exploraremos soluciones.

AFE con Correlaciones Policóricas (Sin Rotar)

Usaremos cor = "poly" y fm="minres" (mínimos cuadrados residuales, no asume normalidad). La opción rotate="none" nos muestra la solución inicial, útil para ver la estructura antes de simplificarla.

fa(datoslw, nfactors = 4, fm = "minres", rotate = "none", cor = "poly")

## Factor Analysis using method =  minres
## Call: fa(r = datoslw, nfactors = 4, rotate = "none", fm = "minres", 
##     cor = "poly")
## Standardized loadings (pattern matrix) based upon correlation matrix
##        MR1   MR2   MR3   MR4   h2     u2 com
## salud 0.78  0.13 -0.17  0.15 0.67 0.3281 1.2
## ingr  0.82  0.30 -0.14  0.22 0.84 0.1611 1.5
## trab  0.85 -0.02 -0.19 -0.08 0.76 0.2350 1.1
## educ  0.89  0.09 -0.12 -0.18 0.84 0.1559 1.1
## vivi  0.88  0.07 -0.04 -0.19 0.81 0.1906 1.1
## segur 0.74  0.35  0.42 -0.03 0.85 0.1471 2.1
## medio 0.80 -0.08  0.17  0.05 0.68 0.3158 1.1
## liber 0.85 -0.48  0.13  0.12 0.99 0.0094 1.7
## proye 0.83 -0.30 -0.02 -0.03 0.78 0.2216 1.3
## 
##                        MR1  MR2  MR3  MR4
## SS loadings           6.18 0.57 0.32 0.16
## Proportion Var        0.69 0.06 0.04 0.02
## Cumulative Var        0.69 0.75 0.79 0.80
## Proportion Explained  0.85 0.08 0.04 0.02
## Cumulative Proportion 0.85 0.93 0.98 1.00
## 
## Mean item complexity =  1.4
## Test of the hypothesis that 4 factors are sufficient.
## 
## df null model =  36  with the objective function =  8.2 with Chi Square =  13004.7
## df of  the model are 6  and the objective function was  0.03 
## 
## The root mean square of the residuals (RMSR) is  0.01 
## The df corrected root mean square of the residuals is  0.02 
## 
## The harmonic n.obs is  1591 with the empirical chi square  4.33  with prob <  0.63 
## The total n.obs was  1591  with Likelihood Chi Square =  42.42  with prob <  1.5e-07 
## 
## Tucker Lewis Index of factoring reliability =  0.983
## RMSEA index =  0.062  and the 90 % confidence intervals are  0.045 0.08
## BIC =  -1.82
## Fit based upon off diagonal values = 1
## Measures of factor score adequacy             
##                                                    MR1  MR2  MR3  MR4
## Correlation of (regression) scores with factors   0.99 0.95 0.82 0.72
## Multiple R square of scores with factors          0.98 0.90 0.67 0.51
## Minimum correlation of possible factor scores     0.95 0.79 0.35 0.02

Interpretación (AFE Policórica, Sin Rotar):

  • Cargas Factoriales (Standardized loadings - pattern matrix): El primer factor (MR1) es un factor general muy fuerte, con cargas altas y positivas en todas las variables (ej. educ 0.89, vivi 0.88, liber 0.85, etc.). Los factores MR2, MR3 y MR4 tienen cargas mucho más bajas y un patrón mixto (algunas positivas, otras negativas como -0.48 de liber en MR2), lo que dificulta su interpretación individual. Esta solución no es simple ni fácilmente interpretable.
  • Varianza Explicada (SS loadings): MR1 explica el 69% de la varianza (Proportion Var). Los 4 factores juntos explican el 80% (Cumulative Var).
  • Índices de Ajuste: El TLI es 0.983 y el RMSEA es 0.062 (IC 90%: 0.045, 0.080). Estos valores sugieren un ajuste de bueno a aceptable del modelo de 4 factores a los datos. El RMSR de 0.01 es muy bueno.

Explorando Rotaciones

Para mejorar la interpretabilidad, aplicaremos rotaciones.

Rotación Ortogonal (Varimax)

Asume que los factores son independientes (no correlacionados).

fa(datoslw, nfactors = 4, fm = "minres", rotate = "varimax", cor = "poly")

## Factor Analysis using method =  minres
## Call: fa(r = datoslw, nfactors = 4, rotate = "varimax", fm = "minres", 
##     cor = "poly")
## Standardized loadings (pattern matrix) based upon correlation matrix
##        MR2  MR4  MR3  MR1   h2     u2 com
## salud 0.35 0.63 0.25 0.31 0.67 0.3281 2.5
## ingr  0.26 0.75 0.37 0.26 0.84 0.1611 2.0
## trab  0.47 0.49 0.21 0.51 0.76 0.2350 3.3
## educ  0.40 0.46 0.34 0.60 0.84 0.1559 3.4
## vivi  0.42 0.40 0.39 0.57 0.81 0.1906 3.6
## segur 0.24 0.31 0.81 0.22 0.85 0.1471 1.7
## medio 0.57 0.34 0.42 0.25 0.68 0.3158 3.0
## liber 0.91 0.25 0.22 0.21 0.99 0.0094 1.4
## proye 0.71 0.30 0.19 0.39 0.78 0.2216 2.2
## 
##                        MR2  MR4  MR3  MR1
## SS loadings           2.46 1.94 1.42 1.41
## Proportion Var        0.27 0.22 0.16 0.16
## Cumulative Var        0.27 0.49 0.65 0.80
## Proportion Explained  0.34 0.27 0.20 0.19
## Cumulative Proportion 0.34 0.61 0.81 1.00
## 
## Mean item complexity =  2.6
## Test of the hypothesis that 4 factors are sufficient.
## 
## df null model =  36  with the objective function =  8.2 with Chi Square =  13004.7
## df of  the model are 6  and the objective function was  0.03 
## 
## The root mean square of the residuals (RMSR) is  0.01 
## The df corrected root mean square of the residuals is  0.02 
## 
## The harmonic n.obs is  1591 with the empirical chi square  4.33  with prob <  0.63 
## The total n.obs was  1591  with Likelihood Chi Square =  42.42  with prob <  1.5e-07 
## 
## Tucker Lewis Index of factoring reliability =  0.983
## RMSEA index =  0.062  and the 90 % confidence intervals are  0.045 0.08
## BIC =  -1.82
## Fit based upon off diagonal values = 1
## Measures of factor score adequacy             
##                                                    MR2  MR4  MR3  MR1
## Correlation of (regression) scores with factors   0.99 0.83 0.87 0.80
## Multiple R square of scores with factors          0.97 0.70 0.75 0.64
## Minimum correlation of possible factor scores     0.94 0.39 0.50 0.29

Interpretación (Rotación Varimax):

  • Cargas Factoriales: La estructura es más clara que sin rotación.
    • MR2 (ahora el más fuerte tras la rotación) agrupa liber (0.91), proye (0.71) y medio (0.57).
    • MR4 agrupa ingr (0.75) y salud (0.63).
    • MR3 está definido principalmente por segur (0.81).
    • MR1 agrupa educ (0.60), vivi (0.57) y trab (0.51).
    • Aún existen algunas cargas cruzadas (ej. trab carga 0.47 en MR2 y 0.51 en MR1; salud 0.35 en MR2 y 0.63 en MR4), lo que significa que estos ítems no se asignan limpiamente a un solo factor. La Mean item complexity de 2.6 indica que, en promedio, los ítems cargan en más de dos factores, lo cual no es ideal para una estructura simple.
  • Varianza Explicada (SS loadings): La varianza total explicada (80%) se ha redistribuido: MR2 (27%), MR4 (22%), MR3 (16%), MR1 (16%).
  • Los índices de ajuste (TLI, RMSEA, etc.) son los mismos que en la solución sin rotar, ya que la rotación no cambia el ajuste global del modelo.

Rotación Oblicua (Promax)

Permite que los factores estén correlacionados, lo cual suele ser más realista en ciencias sociales.

# Ejecutamos el AFE con Promax y lo guardamos como 'modelofinal'
modelofinal <- fa(datoslw, nfactors = 4, fm = "minres", rotate = "promax", cor = "poly")
print(modelofinal) # Imprimimos el resultado completo

## Factor Analysis using method =  minres
## Call: fa(r = datoslw, nfactors = 4, rotate = "promax", fm = "minres", 
##     cor = "poly")
## Standardized loadings (pattern matrix) based upon correlation matrix
##         MR2   MR1   MR4   MR3   h2     u2 com
## salud  0.09  0.13  0.67 -0.04 0.67 0.3281 1.1
## ingr  -0.06 -0.01  0.89  0.10 0.84 0.1611 1.0
## trab   0.17  0.58  0.26 -0.11 0.76 0.2350 1.7
## educ  -0.01  0.76  0.13  0.07 0.84 0.1559 1.1
## vivi   0.05  0.71  0.02  0.17 0.81 0.1906 1.1
## segur -0.03  0.05  0.03  0.89 0.85 0.1471 1.0
## medio  0.51  0.04  0.10  0.28 0.68 0.3158 1.7
## liber  1.11 -0.11 -0.02 -0.02 0.99 0.0094 1.0
## proye  0.67  0.32  0.00 -0.08 0.78 0.2216 1.5
## 
##                        MR2  MR1  MR4  MR3
## SS loadings           2.23 2.14 1.76 1.10
## Proportion Var        0.25 0.24 0.20 0.12
## Cumulative Var        0.25 0.49 0.68 0.80
## Proportion Explained  0.31 0.30 0.24 0.15
## Cumulative Proportion 0.31 0.60 0.85 1.00
## 
##  With factor correlations of 
##      MR2  MR1  MR4  MR3
## MR2 1.00 0.79 0.69 0.61
## MR1 0.79 1.00 0.83 0.68
## MR4 0.69 0.83 1.00 0.70
## MR3 0.61 0.68 0.70 1.00
## 
## Mean item complexity =  1.2
## Test of the hypothesis that 4 factors are sufficient.
## 
## df null model =  36  with the objective function =  8.2 with Chi Square =  13004.7
## df of  the model are 6  and the objective function was  0.03 
## 
## The root mean square of the residuals (RMSR) is  0.01 
## The df corrected root mean square of the residuals is  0.02 
## 
## The harmonic n.obs is  1591 with the empirical chi square  4.33  with prob <  0.63 
## The total n.obs was  1591  with Likelihood Chi Square =  42.42  with prob <  1.5e-07 
## 
## Tucker Lewis Index of factoring reliability =  0.983
## RMSEA index =  0.062  and the 90 % confidence intervals are  0.045 0.08
## BIC =  -1.82
## Fit based upon off diagonal values = 1
## Measures of factor score adequacy             
##                                                    MR2  MR1  MR4  MR3
## Correlation of (regression) scores with factors   1.00 0.96 0.95 0.94
## Multiple R square of scores with factors          0.99 0.92 0.90 0.88
## Minimum correlation of possible factor scores     0.98 0.85 0.81 0.75

Interpretación (Rotación Promax - modelofinal):

  • Cargas Factoriales (Matriz de Patrón - Standardized loadings): Esta es la matriz clave.
    • MR2: Cargas principales y muy altas en liber (1.11), proye (0.67) y medio (0.51). Interpretación tentativa: “Oportunidades de Desarrollo Individual y Entorno”. (La carga >1 en liber es una característica de Promax, indica una fuerte asociación).
    • MR1: Cargas principales en educ (0.76), vivi (0.71) y trab (0.58). proye tiene una carga secundaria aquí (0.32). Interpretación tentativa: “Oportunidades Socioeconómicas Estructurales”.
    • MR4: Cargas principales en ingr (0.89) y salud (0.67). Interpretación tentativa: “Oportunidades de Bienestar Material Básico”.
    • MR3: Carga principal y muy clara en segur (0.89). Interpretación tentativa: Factor de “Seguridad Ciudadana”.
    • La Mean item complexity es 1.2, mucho mejor que con Varimax (2.6), indicando una estructura más simple (ítems cargan predominantemente en un solo factor).
  • Correlación entre Factores (With factor correlations of):
    • MR2 está altamente correlacionado con MR1 (0.79) y MR4 (0.69).
    • MR1 está muy correlacionado con MR4 (0.83).
    • MR3 (Seguridad) está moderadamente correlacionado con los otros (0.61 a 0.70).
    • Estas correlaciones sustanciales (>0.3) entre los factores justifican el uso de una rotación oblicua.
  • Varianza Explicada (Proportion Var): MR2 (25%), MR1 (24%), MR4 (20%), MR3 (12%). La varianza total explicada sigue siendo 80%.
  • Índices de Ajuste: Siguen siendo buenos (TLI=0.983, RMSEA=0.062).

Decisión: El modelo con 4 factores, correlaciones policóricas y rotación Promax (modelofinal) ofrece la solución más interpretable y teóricamente coherente, con buena estructura simple y ajuste.

4. Visualización de la Estructura Factorial

fa.diagram(modelofinal, main = "Diagrama Factorial (4 Factores, Promax, Policórica)")

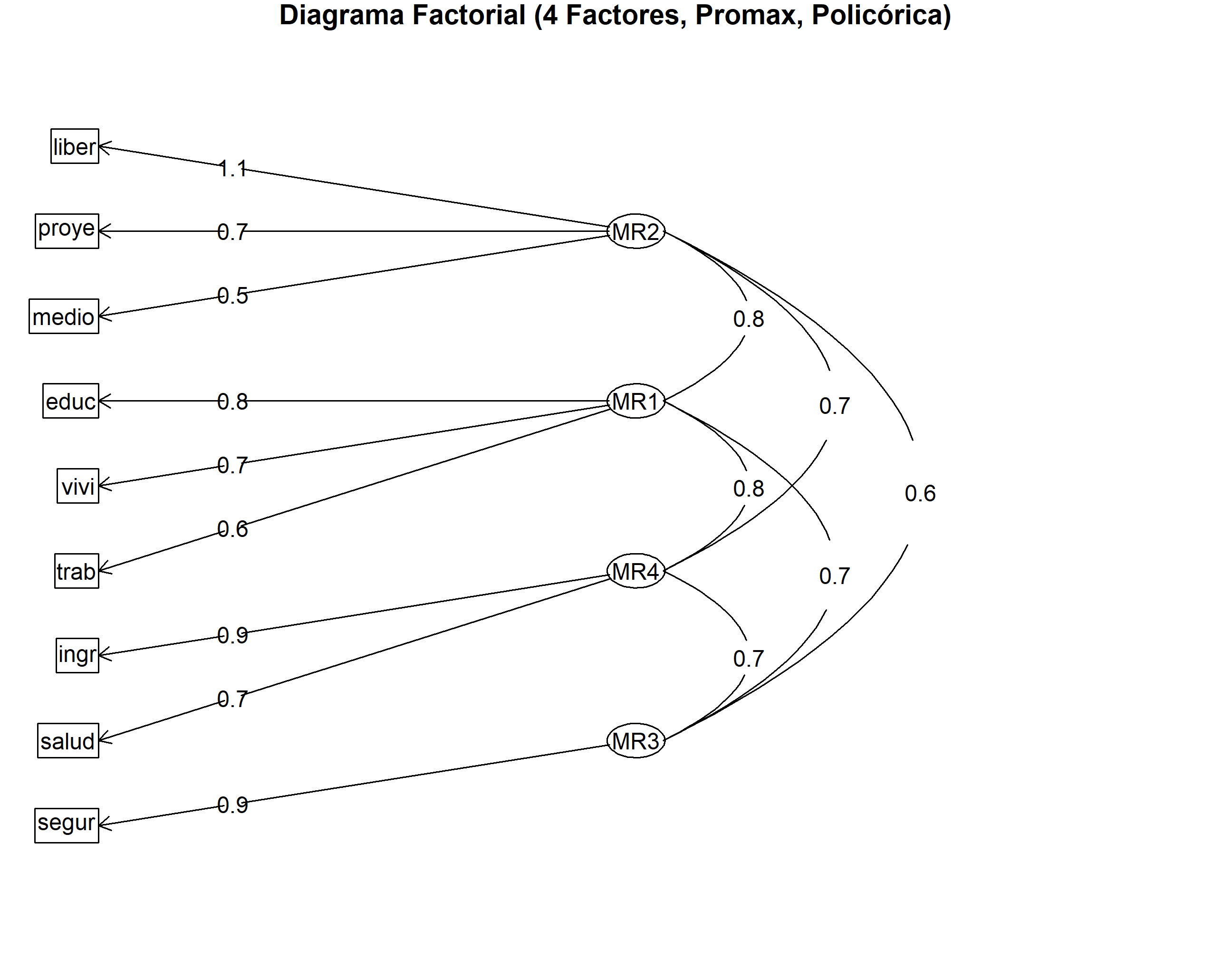Interpretación del Diagrama: El diagrama visualiza las cargas de la matriz de patrón. Las flechas indican la fuerza y dirección de la relación entre cada ítem (rectángulos) y su factor principal (óvalos). Las líneas curvas entre los óvalos representan las correlaciones entre los factores.

  • Se observa que liber, proye, medio se agrupan claramente en MR2.
  • educ, vivi, trab se agrupan en MR1.
  • ingr, salud se agrupan en MR4.
  • segur define MR3. Las correlaciones (ej. 0.79 entre MR2 y MR1; 0.83 entre MR1 y MR4) son evidentes.

5. Cálculo y Exploración de Puntuaciones Factoriales

Calculamos una puntuación para cada individuo en cada uno de los 4 factores.

# Extraer las puntuaciones factoriales del objeto 'modelofinal'
puntuaciones_factoriales <- factor.scores(datoslw, modelofinal, method = "Thurstone") 
# $scores contiene las puntuaciones. Es mejor usar factor.scores() para más control y consistencia

# Resumen de las puntuaciones factoriales (deberían tener media ~0, DE ~1)
summary(puntuaciones_factoriales$scores)

##       MR2               MR1                MR4                MR3          
##  Min.   :-2.2316   Min.   :-1.97324   Min.   :-1.76865   Min.   :-1.59191  
##  1st Qu.:-0.6128   1st Qu.:-0.68464   1st Qu.:-0.72798   1st Qu.:-0.83273  
##  Median : 0.1549   Median : 0.04866   Median : 0.03374   Median :-0.03984  
##  Mean   : 0.0000   Mean   : 0.00000   Mean   : 0.00000   Mean   : 0.00000  
##  3rd Qu.: 0.7362   3rd Qu.: 0.71420   3rd Qu.: 0.72924   3rd Qu.: 0.72964  
##  Max.   : 1.8247   Max.   : 2.02736   Max.   : 2.13972   Max.   : 2.21424

# Unir las puntuaciones factoriales a la base de datos original (que tiene el ID)
# para análisis posteriores, como comparar por GSE.

# Añadir scores a 'datoslw' (que ya no tiene 'cor')
datoslw_con_scores <- bind_cols(datoslw, as.data.frame(puntuaciones_factoriales$scores))

# Añadir la variable 'cor' (ID) que guardamos antes en 'id_casos'
# Esto asegura que cada fila en datoslw_con_scores tenga su ID original
datoslw_con_scores <- datoslw_con_scores %>%
  mutate(cor = id_casos)

# Seleccionar 'cor' y 'GSEo' de la base original 'datosog'
datosog_gse <- datosog %>%
  select(cor, GSEo)

# Unir las puntuaciones y datoslw con la información de GSEo de datosog, usando 'cor' como llave
basefinal <- left_join(datoslw_con_scores, datosog_gse, by = "cor")

# Crear factor para GSE con etiquetas
basefinal <- basefinal %>%
  mutate(gse = factor(GSEo, 
                      levels = 1:4, 
                      labels = c("ABC1", "C2", "C3", "D"),
                      ordered = TRUE)) # Indicamos que es ordinal

# Explorar las medias de las puntuaciones factoriales por Grupo Socioeconómico (GSE)
# usando dplyr para un output más "tidy" y claro
medias_por_gse <- basefinal %>%
  group_by(gse) %>%
  summarise(
    Mean_MR1_Estruc = mean(MR1, na.rm = TRUE),
    Mean_MR2_DesInd = mean(MR2, na.rm = TRUE),
    Mean_MR3_Seg = mean(MR3, na.rm = TRUE),
    Mean_MR4_Bienestar = mean(MR4, na.rm = TRUE)
  )

print(medias_por_gse)

## # A tibble: 5 × 5
##   gse   Mean_MR1_Estruc Mean_MR2_DesInd Mean_MR3_Seg Mean_MR4_Bienestar
##   <ord>           <dbl>           <dbl>        <dbl>              <dbl>
## 1 ABC1            0.696           0.668      0.738               0.683 
## 2 C2              0.105           0.179      0.00992             0.0210
## 3 C3             -0.103          -0.109     -0.153              -0.111 
## 4 D              -0.144          -0.163     -0.0676             -0.0988
## 5 <NA>           -0.336          -0.161     -0.235              -0.295

Interpretación de Puntuaciones Factoriales por GSE: Dando los nombres tentativos a los factores:

  • MR1: Oportunidades Socioeconómicas Estructurales
  • MR2: Oportunidades de Desarrollo Individual y Entorno
  • MR3: Seguridad
  • MR4: Oportunidades de Bienestar Básico

Los resultados muestran:

  • Para todos los factores, existe una clara gradiente socioeconómica. El grupo ABC1 consistentemente presenta las medias más altas (positivas) de percepción de oportunidades.
  • Los grupos C3 y D muestran las medias más bajas (negativas), indicando una percepción menos favorable.
  • El grupo C2 se encuentra en una posición intermedia.
  • Por ejemplo, para MR1 (Estruc.): ABC1 (0.70), C2 (0.11), C3 (-0.10), D (-0.14).
  • Para MR2 (Des. Ind.): ABC1 (0.67), C2 (0.18), C3 (-0.11), D (-0.16).
  • La fila con <NA> en gse (si aparece) corresponde a casos que no pudieron ser mapeados de vuelta, probablemente debido al na.omit() inicial sobre datosog si GSEo tenía NAs. Se filtra para el análisis de medias por GSE.

Conclusión General de Puntuaciones: La estructura factorial encontrada es coherente con la estratificación socioeconómica, validando la relevancia de las dimensiones.

6. Conclusión del Práctico

En este práctico, hemos completado un Análisis Factorial Exploratorio:

  1. Determinamos que 4 factores era el número óptimo a extraer (Análisis Paralelo).
  2. Optamos por correlaciones policóricas y rotación oblicua Promax.
  3. Interpretamos la matriz factorial, identificando 4 factores que explicaron el 80% de la varianza con buen ajuste (TLI=0.983, RMSEA=0.062).
  4. Visualizamos la estructura y calculamos puntuaciones factoriales, observando su asociación con el GSE.

Este proceso permite reducir 9 ítems a 4 dimensiones latentes interpretables.

Previous
Next

Last updated on May 19, 2025