9. Análisis Factorial Confirmatorio (AFC) con `lavaan`

0. Objetivos del Práctico

En este práctico, aprenderemos a realizar un Análisis Factorial Confirmatorio (AFC) utilizando el paquete lavaan en R. El AFC nos permite testear una estructura factorial hipotetizada previamente, basada en la teoría o en resultados de un AFE. Al finalizar, serás capaz de:

Especificar un modelo de medición AFC en la sintaxis de lavaan.
Estimar los parámetros del modelo.
Evaluar el ajuste del modelo a los datos utilizando diversos índices (χ², RMSEA, CFI, TLI).
Interpretar las cargas factoriales estandarizadas y no estandarizadas.
Calcular e interpretar las comunalidades (R² de los indicadores).
Explorar los índices de modificación para posibles re-especificaciones del modelo.

1. Carga de Paquetes y Datos

Primero, cargamos los paquetes necesarios. lavaan es el paquete central para AFC y SEM. semPlot (si está disponible) nos permitirá visualizar el modelo.

# Carga paquetes
# install.packages(c("haven", "lavaan", "dplyr", "semPlot", "texreg")) # Descomentar si es necesario

# # 1) URL del binario para la rama 4.4 de R (Ejemplo para OpenMx, adaptar si es necesario para otras dependencias de semPlot)
# mx_url <- "https://cran.r-project.org/bin/windows/contrib/4.4/OpenMx_2.21.13.zip"
# 
# # 2) Instalar sin compilar
# install.packages(mx_url,
#                  repos = NULL,
#                  type  = "win.binary")
# install.packages("RcppParallel") # Otra dependencia común

library(haven)    # Para importar datos SPSS, Stata, etc.
library(lavaan)   # Para estimar AFC y SEM
library(dplyr)    # Para manipulación de datos (opcional aquí, pero buena práctica)
library(semPlot)  # Para graficar modelos SEM (si no está disponible, esta parte se puede omitir o usar alternativas)
library(texreg)   # Para tablas de resultados bien formateadas

Nota sobre semPlot: Si tienes problemas para instalar semPlot directamente desde CRAN (ya que ha sido archivado), puedes intentar instalarlo desde GitHub con devtools::install_github("SachaEpskamp/semPlot") o buscar versiones archivadas. Si no es posible, las secciones de gráficos pueden omitirse o adaptarse.

A continuación, importamos los datos. Usaremos una base de ejemplo sobre ideología que contiene ítems para medir “autoritarismo” y “dominancia social”.

Item	Etiqueta
dom1	Los grupos inferiores debieran quedarse en su lugar
dom2	Si algunos grupos se mantuvieran en su lugar, tendríamos menos problemas
dom3	A veces es necesario pasar por encima de algunos grupos para surgir en la vida
aut1	Las formas y valores tradicionales aún son la mejor manera de vivir
aut2	Es importante que mantengamos los valores y estándares morales tradicionales
aut3	Este país va a prosperar si los jóvenes dejan de experimentar con drogas, alcohol y sexo, y prestan más atención a los valores familiares

# Importar datos desde una URL (GitHub)
datos <- read_sav(url("https://github.com/Clases-GabrielSotomayor/pruebapagina/raw/master/content/example/input/data/base_ideologia_afc.sav"))

# Vistazo rápido a los datos y sus nombres
# glimpse(datos) # Comentado para brevedad
# head(datos)    # Comentado para brevedad

2. Especificación del Modelo de Medición

Definimos nuestro modelo teórico. Hipotetizamos dos factores latentes:

autoritarismo: medido por los ítems aut1, aut2, aut3.
dominancia: medido por los ítems dom1, dom2, dom3.

En la sintaxis de lavaan, el operador =~ (“es medido por”) define esta relación.

# Definir el modelo de medición para el AFC
mod_conf <- '
  # Factor latente de Autoritarismo y sus indicadores
  autoritarismo =~ aut1 + aut2 + aut3

  # Factor latente de Dominancia Social y sus indicadores
  dominancia    =~ dom1 + dom2 + dom3
  
  # Por defecto, lavaan estima la covarianza entre factores latentes si hay más de uno.
'
# Imprimimos la especificación para verificar
# cat(mod_conf) # Comentado para brevedad

3. Estimación del Modelo AFC

Con el modelo especificado, usamos la función cfa() de lavaan para estimar los parámetros.

# Ajustar el modelo AFC a los datos
mod_conf_afc <- cfa(model = mod_conf, data = datos)

El objeto mod_conf_afc ahora contiene todos los resultados de la estimación.

4. Evaluación de los Resultados del Modelo

Usamos summary() para obtener un resumen completo, solicitando medidas de ajuste y soluciones estandarizadas.

# Obtener un resumen completo del modelo ajustado
summary_output <- summary(mod_conf_afc,
                          standardized = TRUE, # Mostrar cargas estandarizadas (Std.all)
                          fit.measures = TRUE, # Mostrar un conjunto extendido de índices de ajuste
                          rsquare = TRUE)      # Mostrar R-cuadrado para variables observadas (comunalidades)

print(summary_output)

## lavaan 0.6.15 ended normally after 29 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        13
## 
##   Number of observations                           176
## 
## Model Test User Model:
##                                                       
##   Test statistic                                12.332
##   Degrees of freedom                                 8
##   P-value (Chi-square)                           0.137
## 
## Model Test Baseline Model:
## 
##   Test statistic                               650.010
##   Degrees of freedom                                15
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.993
##   Tucker-Lewis Index (TLI)                       0.987
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)              -1682.172
##   Loglikelihood unrestricted model (H1)             NA
##                                                       
##   Akaike (AIC)                                3390.345
##   Bayesian (BIC)                              3431.561
##   Sample-size adjusted Bayesian (SABIC)       3390.393
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.055
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.113
##   P-value H_0: RMSEA <= 0.050                    0.384
##   P-value H_0: RMSEA >= 0.080                    0.282
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.049
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   autoritarismo =~                                                      
##     aut1              1.000                               1.646    0.907
##     aut2              0.921    0.060   15.457    0.000    1.517    0.887
##     aut3              0.929    0.069   13.502    0.000    1.530    0.803
##   dominancia =~                                                         
##     dom1              1.000                               1.201    0.919
##     dom2              1.096    0.080   13.729    0.000    1.316    0.882
##     dom3              0.861    0.084   10.298    0.000    1.034    0.685
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   autoritarismo ~~                                                      
##     dominancia        0.678    0.174    3.891    0.000    0.343    0.343
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .aut1              0.582    0.129    4.504    0.000    0.582    0.177
##    .aut2              0.623    0.117    5.319    0.000    0.623    0.213
##    .aut3              1.291    0.170    7.598    0.000    1.291    0.356
##    .dom1              0.264    0.083    3.181    0.001    0.264    0.155
##    .dom2              0.494    0.108    4.585    0.000    0.494    0.222
##    .dom3              1.209    0.142    8.484    0.000    1.209    0.531
##     autoritarismo     2.711    0.364    7.454    0.000    1.000    1.000
##     dominancia        1.442    0.196    7.360    0.000    1.000    1.000
## 
## R-Square:
##                    Estimate
##     aut1              0.823
##     aut2              0.787
##     aut3              0.644
##     dom1              0.845
##     dom2              0.778
##     dom3              0.469

Interpretación de la Salida de summary():

Encabezado: lavaan 0.6-19 ended normally after 29 iterations. El modelo convergió. Se usó el estimador ML (Máxima Verosimilitud). Number of observations 176.
Latent Variables:
- autoritarismo =~:
  - aut1: Carga no estandarizada fijada a 1.000. Carga estandarizada (Std.all) = 0.907.
  - aut2: Carga estandarizada (Std.all) = 0.887. Es significativa (P(>|z|) = 0.000).
  - aut3: Carga estandarizada (Std.all) = 0.803. Es significativa (P(>|z|) = 0.000).
  - Todos los indicadores muestran cargas estandarizadas muy altas (>0.80) y significativas sobre el factor “autoritarismo”, sugiriendo que son buenos medidores de este constructo.
- dominancia =~:
  - dom1: Carga no estandarizada fijada a 1.000. Carga estandarizada (Std.all) = 0.919.
  - dom2: Carga estandarizada (Std.all) = 0.882. Es significativa (P(>|z|) = 0.000).
  - dom3: Carga estandarizada (Std.all) = 0.685. Es significativa (P(>|z|) = 0.000).
  - Los indicadores dom1 y dom2 son excelentes medidores de “dominancia”. dom3 tiene una carga un poco más baja pero aún sustancial y aceptable.
Covariances:
- autoritarismo ~~ dominancia: La covarianza estimada es 0.678. La correlación estandarizada (Std.all) entre los dos factores latentes es 0.343. Esta correlación es positiva, moderada y estadísticamente significativa (P(>|z|) = 0.000), indicando que “autoritarismo” y “dominancia social” son constructos relacionados pero distintos.
Variances: Muestra las varianzas de los errores de los indicadores (ej. .aut1 = 0.582) y las varianzas estimadas de los factores latentes (autoritarismo = 2.711, dominancia = 1.442 en la escala no estandarizada).
R-Square (Comunalidades):
- aut1: 0.823 (82.3% de su varianza es explicada por el factor “autoritarismo”)
- aut2: 0.787 (78.7%)
- aut3: 0.644 (64.4%)
- dom1: 0.845 (84.5% de su varianza es explicada por el factor “dominancia”)
- dom2: 0.778 (77.8%)
- dom3: 0.469 (46.9%)
- Todas las comunalidades son de moderadas a altas, indicando que los factores explican una buena proporción de la varianza de sus respectivos indicadores. dom3 es el que tiene la comunalidad más baja (46.9%), lo que significa que casi la mitad de su varianza no es explicada por el factor “dominancia”.

Índices de Ajuste Específicos

Podemos solicitar un conjunto específico de índices de ajuste.

# Ver solo los índices de ajuste seleccionados
fitMeasures(mod_conf_afc,
            fit.measures = c("chisq", "df", "pvalue", # Prueba Chi-cuadrado
                             "cfi", "tli",             # Índices Comparativos
                             "rmsea", "rmsea.ci.lower", "rmsea.ci.upper", # RMSEA y su IC 90%
                             "srmr"))                   # Standardized Root Mean Square Residual

##          chisq             df         pvalue            cfi            tli 
##         12.332          8.000          0.137          0.993          0.987 
##          rmsea rmsea.ci.lower rmsea.ci.upper           srmr 
##          0.055          0.000          0.113          0.049

Interpretación de los Índices de Ajuste:

chisq = 12.332, df = 8, pvalue = 0.137:
- El p-valor (0.137) es mayor que 0.05, por lo que no rechazamos la hipótesis nula de que el modelo se ajusta perfectamente a los datos poblacionales. Este es un buen indicador de ajuste.
- $\chi^2/gl = 12.332 / 8 \approx 1.54$. Este valor está por debajo de 2, lo que sugiere un excelente ajuste según este criterio menos estricto.
cfi = 0.993: Valor muy cercano a 1 (y > 0.95), indica un excelente ajuste comparativo.
tli = 0.987: También muy cercano a 1 (y > 0.95), indica un excelente ajuste comparativo.
rmsea = 0.055:
- Este valor está en el límite entre “buen ajuste” ($\leq 0.05$) y “ajuste razonable” (0.05-0.08).
- IC 90% para RMSEA (rmsea.ci.lower, rmsea.ci.upper): 0.000 - 0.113. El intervalo es algo amplio e incluye valores por encima de 0.08 (incluso 0.10), lo que modera un poco el optimismo. El límite inferior en 0 es bueno. La prueba de que RMSEA $\leq 0.05$ tiene un p-valor de 0.384 (no podemos rechazar que sea $\leq 0.05$).
srmr = 0.049: Este valor es menor que 0.08 (e incluso < 0.05), lo que indica un muy buen ajuste en términos de los residuos estandarizados promedio.

Conclusión General del Ajuste: El modelo de dos factores propuesto muestra un ajuste general de bueno a excelente a los datos, según la mayoría de los índices. El $\chi^2$ no es significativo, el $\chi^2/gl$ es bajo, CFI y TLI son muy altos, y SRMR es bajo. El RMSEA es aceptable, aunque su intervalo de confianza es un poco amplio.

5. Visualización del Modelo (usando `semPlot`)

semPaths puede graficar el modelo, mostrando las cargas estandarizadas.

# Diagrama del modelo con cargas estandarizadas
semPlot::semPaths(mod_conf_afc, 
                    what = "std",  # Mostrar cargas estandarizadas (Std.all)
                    whatLabels = "std", 
                    residuals = TRUE, 
                    intercepts = FALSE, 
                    edge.color = "black"
                  ) # Márgenes

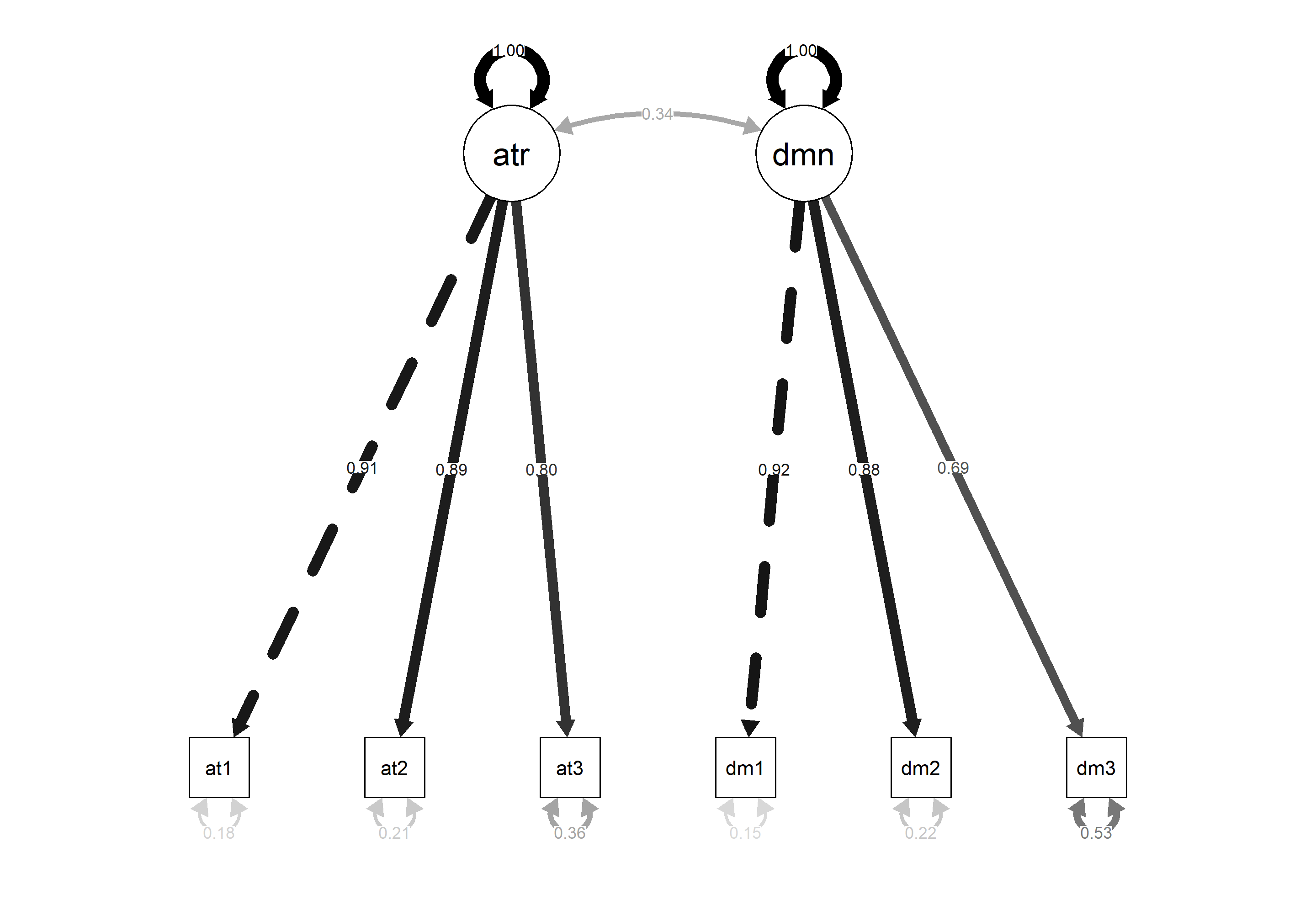Interpretación del Gráfico: El diagrama visualiza el modelo teórico. Las flechas desde los óvalos (factores latentes autoritarismo y dominancia) a los rectángulos (ítems aut1-3 y dom1-3) muestran las cargas factoriales estandarizadas (Std.all). La línea curva entre autoritarismo y dominancia representa su correlación (0.343). Las pequeñas flechas hacia cada ítem indican sus varianzas de error (1 - R²). Este gráfico confirma visualmente que todos los ítems cargan sustancialmente en sus factores designados y que los factores están moderadamente correlacionados.

6. Comunalidades (R-cuadrado de los Indicadores)

Las comunalidades indican qué proporción de la varianza de cada ítem es explicada por el factor latente en el que carga.

# Obtener R-cuadrado (comunalidades) para las variables observadas
inspect(mod_conf_afc, what = "rsquare")

##  aut1  aut2  aut3  dom1  dom2  dom3 
## 0.823 0.787 0.644 0.845 0.778 0.469

Interpretación:

aut1: 0.823 (El factor autoritarismo explica el 82.3% de la varianza de aut1).
aut2: 0.787 (78.7%)
aut3: 0.644 (64.4%)
dom1: 0.845 (El factor dominancia explica el 84.5% de la varianza de dom1).
dom2: 0.778 (77.8%)
dom3: 0.469 (46.9%) Todas las comunalidades son buenas (mayores a 0.40, y la mayoría > 0.60). El ítem dom3 es el que tiene la comunalidad más baja (46.9%), lo que significa que más de la mitad de su varianza es única o error. Sin embargo, dado que su carga factorial (0.685) sigue siendo aceptable, y el modelo general ajusta bien, podría mantenerse.

7. Índices de Modificación (Para Explorar Mejoras)

Los índices de modificación (IM) sugieren cambios al modelo que podrían mejorar significativamente su ajuste. Deben usarse con mucha cautela y siempre con justificación teórica.

# Mostrar los IM más altos, ordenados (IM > 3.84 es aprox. p<0.05 con 1gl)
mod_indices <- modificationindices(mod_conf_afc, sort. = TRUE, minimum.value = 3.84) 
print(head(mod_indices, 10))

##              lhs op  rhs    mi    epc sepc.lv sepc.all sepc.nox
## 18 autoritarismo =~ dom3 6.437 -0.152  -0.250   -0.165   -0.165
## 34          dom1 ~~ dom2 6.437 -0.982  -0.982   -2.719   -2.719
## 30          aut2 ~~ dom3 4.180 -0.170  -0.170   -0.196   -0.196

Interpretación: La salida muestra los 3 cambios que superarían el umbral de 3.84 para el índice de modificación (mi):

autoritarismo =~ dom3 (mi = 6.437): Sugiere que el ítem dom3 (originalmente solo de dominancia) también podría cargar en el factor autoritarismo. El cambio esperado en el parámetro (epc) sería -0.152.
dom1 ~~ dom2 (mi = 6.437): Sugiere correlacionar los errores de los ítems dom1 y dom2. Esto implicaría que estos dos ítems comparten varianza específica no explicada por el factor dominancia (quizás por una redacción muy similar o un aspecto muy particular que miden juntos). El epc es -0.982 (para la covarianza).
aut2 ~~ dom3 (mi = 4.180): Sugiere correlacionar los errores de aut2 y dom3. Consideraciones Teóricas:

¿Es teóricamente plausible que dom3 mida también autoritarismo? Podría ser, dependiendo de su contenido exacto.
¿Hay una razón teórica para que los errores de dom1 y dom2 (o aut2 y dom3) estén correlacionados más allá de sus factores? Decisión: Dado el ya buen ajuste del modelo, estas modificaciones podrían no ser necesarias a menos que haya una fuerte justificación teórica. El IM más alto (6.437) no es extremadamente grande. En este caso, podríamos optar por mantener el modelo original por su parsimonia y buen ajuste general.

8. Conclusión

En este práctico, hemos:

Especificado y estimado un modelo AFC de dos factores con lavaan.
Evaluado el ajuste del modelo, encontrando que es bueno a excelente según la mayoría de los índices (χ² no significativo, $\chi^2/gl \approx 1.54$, CFI/TLI > 0.98, SRMR < 0.05, RMSEA = 0.055).
Interpretado las cargas factoriales estandarizadas, que fueron todas altas y significativas, y la correlación positiva y moderada (0.343) entre los factores.
Revisado las comunalidades, que en general fueron buenas, con dom3 como el ítem con menor varianza explicada.
Explorado los índices de modificación, que no sugirieron cambios urgentes o teóricamente obvios dado el buen ajuste inicial.

El AFC nos ha permitido confirmar que la estructura de dos factores correlacionados (autoritarismo y dominancia) representa bien los datos de estos seis ítems.

Last updated on June 7, 2025