10. AFC con Datos de Encuesta Compleja

0. Objetivos del Práctico

En el práctico anterior, aprendimos los fundamentos del Análisis Factorial Confirmatorio (AFC) con un conjunto de datos ideal. En este práctico, daremos un paso crucial hacia la aplicación en el mundo real, utilizando datos de una encuesta nacional con un diseño muestral complejo. El objetivo es ir más allá de la simple estimación y abordar los desafíos que surgen al trabajar con datos reales.

Al finalizar, serás capaz de:

Aplicar un flujo de trabajo completo de AFC, desde la preparación de los datos hasta la interpretación final.
Manejar y codificar valores perdidos de manera apropiada.
Estimar modelos AFC con variables ordinales, utilizando el estimador correcto (WLSMV).
Comparar modelos teóricos alternativos (unifactorial vs. bifactorial) para determinar la mejor estructura latente.
Incorporar un diseño muestral complejo (ponderadores, estratos y conglomerados) para obtener estimaciones de parámetros, errores estándar e índices de ajuste generalizables y estadísticamente válidos.

1. Carga de Paquetes y Nota sobre `lavaan.survey`

Una Nota Importante Sobre `lavaan.survey`

Antes de comenzar, es crucial abordar el estado del paquete lavaan.survey. Este paquete fue “archivado” en CRAN (el repositorio oficial de R) en 2023. Esto ocurrió porque, tras actualizaciones de R y del propio lavaan, algunas de sus pruebas automáticas internas comenzaron a fallar por diferencias numéricas muy pequeñas, y el autor no actualizó el paquete para corregirlas.

Este es un ejemplo real y práctico de los desafíos del software de código abierto: los paquetes pueden quedar sin mantenimiento. Para este curso, seguiremos usándolo por su gran valor pedagógico para enseñar el flujo de trabajo con encuestas complejas. Lo instalaremos desde un “espejo” en GitHub, pero es importante que seas consciente de que para futuros proyectos de investigación, deberías verificar el estado del paquete y considerar las alternativas mencionadas en el texto de la clase.

# Como lavaan.survey fue archivado de CRAN, lo instalamos desde un mirror en GitHub
# Esto podría requerir el paquete 'remotes'. Si no lo tienes, instálalo primero.
# install.packages("remotes")
remotes::install_github("cran/lavaan.survey")

Ahora, cargamos todos los paquetes que usaremos en este práctico.

# Cargar paquetes necesarios. Pacman los instala si no están presentes.
if (!require("pacman")) install.packages("pacman")
pacman::p_load(haven, survey, lavaan, lavaan.survey, dplyr, texreg, semPlot)

2. El Caso de Estudio: Escala PHQ-4 y Datos EBS 2023

Nuestro caso de estudio es la validación de la estructura factorial de la escala Patient Health Questionnaire-4 (PHQ-4), una herramienta de tamizaje ultra-breve para la ansiedad y la depresión. Utilizaremos los datos de la Encuesta de Bienestar Social (EBS) 2023 de Chile.

La escala PHQ-4 consta de 4 ítems: dos para depresión y dos para ansiedad.

Ítem EBS	Constructo	Pregunta	Opciones de Respuesta
`ss7_a`	Depresión	¿Poco interés o placer en hacer cosas?	1-4 (Nunca a Casi todos los días)
`ss7_b`	Depresión	¿Se ha sentido decaído(a), deprimido(a) o sin esperanzas?	1-4 (Nunca a Casi todos los días)
`ss7_c`	Ansiedad	¿Se ha sentido nervioso(a), ansioso(a) o con los nervios de punta?	1-4 (Nunca a Casi todos los días)
`ss7_d`	Ansiedad	¿No ha sido capaz de parar o controlar su preocupación?	1-4 (Nunca a Casi todos los días)

# Cargar datos de la EBS 2023 desde la URL
tmp <- tempfile(fileext = ".RData")
download.file(
  "https://github.com/GabrielSotomayorl/aadii2025/raw/refs/heads/main/static/data/Base%20de%20datos%20EBS%202023.RData",
  tmp, mode = "wb"
)
ebs <- get(load(tmp))
unlink(tmp); rm(tmp)

3. Preparación y Limpieza de Datos

El trabajo con datos reales casi siempre requiere una fase de limpieza. Nuestros pasos serán:

Seleccionar las variables de interés.
Codificar los valores perdidos (-88 y -99) como NA.
Recodificar los ítems de 1-4 a 0-3 para facilitar la interpretación.
Gestionar los casos perdidos (usaremos análisis de casos completos con na.omit()).

# 1. Nombres de las variables de interés
phq4_vars <- c("ss7_a", "ss7_b", "ss7_c", "ss7_d")
design_vars <- c("varunit", "estrato_ebs", "fexp")

# 2. Seleccionar y limpiar los datos
ebs_limpia <- ebs %>%
  select(all_of(phq4_vars), all_of(design_vars)) %>%
  mutate(across(all_of(phq4_vars), ~na_if(., -88))) %>% # Convertir -88 a NA
  mutate(across(all_of(phq4_vars), ~na_if(., -99))) %>% # Convertir -99 a NA
  # 3. Recodificar ítems de 1-4 a 0-3 (0 = Nunca, 3 = Casi todos los días)
  mutate(across(all_of(phq4_vars), ~.x - 1)) %>%
  # 4. Eliminar filas con cualquier NA en los ítems PHQ-4 para el análisis
  na.omit()

# Verificar cantidad de datos perdidos eliminados
cat("Número de casos originales:", nrow(ebs), "\n")

## Número de casos originales: 11234

cat("Número de casos completos para el análisis:", nrow(ebs_limpia), "\n")

## Número de casos completos para el análisis: 11215

Observamos que solo se perdieron 19 casos (11234 - 11215), por lo que proceder con casos completos es una estrategia razonable aquí.

4. Especificación y Comparación de Modelos

Nuestra pregunta teórica es: ¿la escala PHQ-4 mide un único constructo de “malestar psicológico” o dos constructos distintos pero relacionados de “depresión” y “ansiedad”? Para responder, especificaremos y compararemos dos modelos.

# Modelo 1: Un solo factor de malestar psicológico
mod_phq4_1f <- '
  malestar =~ ss7_a + ss7_b + ss7_c + ss7_d
'

# Modelo 2: Dos factores correlacionados (Depresión y Ansiedad)
mod_phq4_2f <- '
  depresion =~ ss7_a + ss7_b
  ansiedad  =~ ss7_c + ss7_d
'

Estimaremos ambos modelos usando el estimador WLSMV, adecuado para variables ordinales, e incorporando los pesos muestrales (fexp).

# Vector con los nombres de los ítems a tratar como ordinales
items_ordinales <- c("ss7_a", "ss7_b", "ss7_c", "ss7_d")

# Estimar Modelo 1 (Unifactorial)
fit_1f <- cfa(mod_phq4_1f, 
              data = ebs_limpia, 
              ordered = items_ordinales,
              sampling.weights = "fexp",
              estimator = "WLSMV")

# Estimar Modelo 2 (Bifactorial)
fit_2f <- cfa(mod_phq4_2f, 
              data = ebs_limpia, 
              ordered = items_ordinales,
              sampling.weights = "fexp",
              estimator = "WLSMV")

Ahora, comparamos formalmente ambos modelos.

# Comparar los dos modelos
anova(fit_1f, fit_2f)

## 
## Scaled Chi-Squared Difference Test (method = "satorra.2000")
## 
## lavaan NOTE:
##     The "Chisq" column contains standard test statistics, not the
##     robust test that should be reported per model. A robust difference
##     test is a function of two standard (not robust) statistics.
##  
##        Df AIC BIC    Chisq Chisq diff Df diff Pr(>Chisq)    
## fit_2f  1           4.2477                                  
## fit_1f  2         106.3918     217.58       1  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretación de la Comparación: La prueba de diferencia de Chi-cuadrado escalada nos permite decidir qué modelo es superior. El resultado es inequívoco:

Chisq diff = 217.58: La diferencia en el ajuste entre los modelos es extremadamente grande.
Df diff = 1: Esta diferencia se evalúa con 1 grado de libertad.
Pr(>Chisq) < 2.2e-16 ***: El p-valor es prácticamente cero. Conclusión: Rechazamos de forma contundente la hipótesis nula de que ambos modelos se ajustan igual de bien. El modelo más complejo (el de dos factores, fit_2f) ofrece una mejora de ajuste estadísticamente muy significativa en comparación con el modelo de un solo factor. Esto nos da una fuerte evidencia empírica para preferir la estructura de dos dimensiones (Depresión y Ansiedad) para la escala PHQ-4.

5. Análisis en Profundidad del Modelo Seleccionado (2 Factores)

Habiendo elegido el modelo de dos factores, ahora debemos corregir sus errores estándar e índices de ajuste para reflejar el diseño muestral completo de la EBS.

# 1. Crear el objeto de diseño de encuesta con los datos limpios
diseno_ebs <- svydesign(
  id = ~varunit, 
  strata = ~estrato_ebs, 
  weights = ~fexp, 
  data = ebs_limpia)

# 2. Corregir el modelo lavaan usando el diseño de encuesta
fit_2f_complejo <- lavaan.survey(
  lavaan.fit = fit_2f, 
  survey.design = diseno_ebs)

Ahora sí, solicitamos el resumen final y definitivo.

# 3. Obtener el resumen completo y corregido
summary(fit_2f_complejo, 
        standardized = TRUE, 
        fit.measures = TRUE, 
        rsquare = TRUE)

## lavaan 0.6.15 ended normally after 24 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        13
## 
##   Number of observations                         11215
## 
## Model Test User Model:
##                                               Standard      Scaled
##   Test Statistic                                31.575      11.367
##   Degrees of freedom                                 1           1
##   P-value (Chi-square)                           0.000       0.001
##   Scaling correction factor                                  2.778
##     Satorra-Bentler correction                                    
## 
## Model Test Baseline Model:
## 
##   Test statistic                             16100.926    4583.320
##   Degrees of freedom                                 6           6
##   P-value                                        0.000       0.000
##   Scaling correction factor                                  3.513
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.998       0.998
##   Tucker-Lewis Index (TLI)                       0.989       0.986
##                                                                   
##   Robust Comparative Fit Index (CFI)                         0.998
##   Robust Tucker-Lewis Index (TLI)                            0.989
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)             -52539.298  -52539.298
##   Loglikelihood unrestricted model (H1)     -52523.510  -52523.510
##                                                                   
##   Akaike (AIC)                              105104.595  105104.595
##   Bayesian (BIC)                            105199.821  105199.821
##   Sample-size adjusted Bayesian (SABIC)     105158.508  105158.508
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.052       0.030
##   90 Percent confidence interval - lower         0.038       0.021
##   90 Percent confidence interval - upper         0.069       0.040
##   P-value H_0: RMSEA <= 0.050                    0.373       1.000
##   P-value H_0: RMSEA >= 0.080                    0.002       0.000
##                                                                   
##   Robust RMSEA                                               0.051
##   90 Percent confidence interval - lower                     0.027
##   90 Percent confidence interval - upper                     0.079
##   P-value H_0: Robust RMSEA <= 0.050                         0.423
##   P-value H_0: Robust RMSEA >= 0.080                         0.043
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.006       0.006
## 
## Parameter Estimates:
## 
##   Standard errors                           Robust.sem
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   depresion =~                                                          
##     ss7_a             1.000                               0.663    0.713
##     ss7_b             1.190    0.030   39.316    0.000    0.789    0.875
##   ansiedad =~                                                           
##     ss7_c             1.000                               0.779    0.805
##     ss7_d             0.810    0.020   41.159    0.000    0.631    0.673
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##   depresion ~~                                                          
##     ansiedad          0.449    0.015   30.302    0.000    0.870    0.870
## 
## Intercepts:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .ss7_a             0.928    0.013   73.871    0.000    0.928    0.999
##    .ss7_b             0.825    0.012   67.857    0.000    0.825    0.916
##    .ss7_c             0.947    0.013   73.194    0.000    0.947    0.979
##    .ss7_d             0.663    0.013   51.899    0.000    0.663    0.707
##     depresion         0.000                               0.000    0.000
##     ansiedad          0.000                               0.000    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
##    .ss7_a             0.424    0.016   26.747    0.000    0.424    0.491
##    .ss7_b             0.190    0.014   13.408    0.000    0.190    0.234
##    .ss7_c             0.330    0.016   20.770    0.000    0.330    0.352
##    .ss7_d             0.481    0.019   25.665    0.000    0.481    0.547
##     depresion         0.439    0.019   23.191    0.000    1.000    1.000
##     ansiedad          0.607    0.021   28.985    0.000    1.000    1.000
## 
## R-Square:
##                    Estimate
##     ss7_a             0.509
##     ss7_b             0.766
##     ss7_c             0.648
##     ss7_d             0.453

Interpretación de los Resultados del Modelo Final:

Índices de Ajuste:
- Test Chi-cuadrado (Scaled): El valor es 11.367 con 1 gl, y un p-valor de 0.001. A pesar de que el p-valor es significativo (lo que indica un desajuste estadísticamente significativo), esto es esperable en muestras muy grandes (N=11,215), donde la prueba tiene un poder enorme para detectar discrepancias triviales. Por ello, nos fiamos más de los otros índices.
- CFI/TLI: El Robust CFI = 0.998 y el Robust TLI = 0.989. Ambos valores son excelentes, muy por encima del umbral de 0.95, lo que indica un ajuste comparativo casi perfecto.
- RMSEA: El Robust RMSEA = 0.051. Este valor es muy bueno, situándose en el límite del criterio estricto (≤ 0.05). Su intervalo de confianza al 90% [0.027, 0.079] es estrecho y se encuentra completamente por debajo del umbral de mal ajuste (0.08).
- SRMR = 0.006: Este valor es extremadamente bajo, indicando que, en promedio, los residuos estandarizados son muy pequeños.
- Conclusión de Ajuste: En conjunto, a pesar del Chi-cuadrado significativo, los demás índices (CFI, TLI, RMSEA, SRMR) señalan un excelente ajuste del modelo de dos factores a los datos.
Parámetros del Modelo:
- Cargas Factoriales (Std.all):
  - Depresión: El ítem ss7_a (“poco interés”) tiene una carga de 0.713 y ss7_b (“sentirse decaído”) tiene una carga de 0.875. Ambas son muy fuertes y significativas.
  - Ansiedad: El ítem ss7_c (“sentirse nervioso”) carga 0.805 y ss7_d (“no controlar preocupación”) carga 0.673. Nuevamente, ambas son sustanciales y significativas, aunque ss7_d es un indicador ligeramente más débil que los otros tres.
- Correlación entre Factores (Std.all):
  - La correlación entre los factores latentes depresion y ansiedad es de 0.870. Esta es una correlación muy alta y positiva, lo que es teóricamente esperable dada la alta comorbilidad entre ambos constructos. Indica que, aunque son estadísticamente separables, en la práctica se superponen enormemente.
- Comunalidades (R-Square):
  - ss7_a: 50.9% de su varianza es explicada por el factor “depresión”.
  - ss7_b: 76.6% (excelente).
  - ss7_c: 64.8% (muy bueno).
  - ss7_d: 45.3%.
  - Los ítems ss7_b y ss7_c son los indicadores más “puros” de sus respectivos factores. ss7_d es el más débil, con más de la mitad de su varianza siendo única o error de medición.

6. Visualización del Modelo Final

# Graficar el modelo original (fit_2f). Los valores de los parámetros son los correctos.
semPlot::semPaths(fit_2f, 
                  what = "std",
                  whatLabels = "std",
                  residuals = TRUE, 
                  intercepts = FALSE, 
                  edge.color = "black",
                  layout = "tree2")

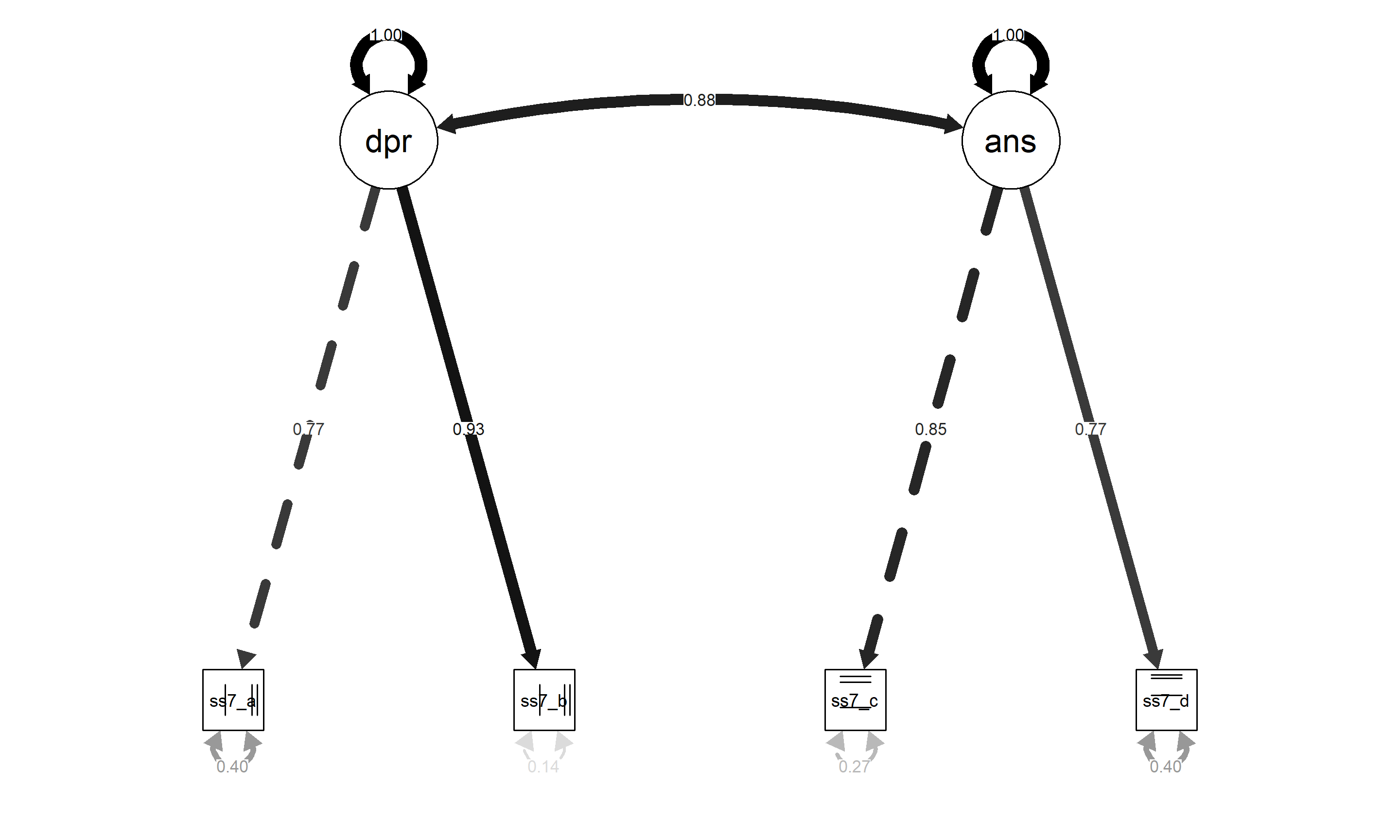
Interpretación del Gráfico: El diagrama visualiza claramente la estructura del modelo. Vemos los dos factores latentes (círculos) y sus respectivos indicadores (rectángulos). Las flechas muestran las cargas estandarizadas, confirmando visualmente que ss7_b (0.875) y ss7_c (0.805) son los indicadores más fuertes. Lo más destacable es la línea curva gruesa entre depresion y ansiedad con el valor 0.87, ilustrando la altísima correlación entre ambos constructos.

7. Conclusión General

En este práctico, hemos realizado un análisis factorial confirmatorio de principio a fin utilizando datos reales de una encuesta compleja. El proceso nos llevó a:

Preparar y limpiar una base de datos real, manejando valores perdidos.
Comparar formalmente dos modelos teóricos, concluyendo que una estructura de dos factores (Depresión y Ansiedad) es empíricamente superior a una de un solo factor.
Aplicar correctamente las correcciones por diseño muestral complejo, obteniendo resultados válidos y generalizables.
Interpretar en detalle un modelo final, que mostró un ajuste excelente, cargas factoriales robustas y una correlación muy alta entre los factores latentes.

Este ejercicio demuestra el poder del AFC no solo para “confirmar” una teoría, sino para testear activamente hipótesis rivales y manejar las complejidades inherentes a los datos de las ciencias sociales.

Last updated on June 7, 2025