Introducción a los Modelos Multivariados
Sesión 6: Fundamentos, Repaso Estadístico y Regresión Lineal Múltiple
2025-04-21
Objetivos de la Sesión
En esta sesión, construiremos las bases para el análisis multivariado:
- Entender por qué usamos modelos multivariados en sociología y sus funciones principales.
- Diferenciar entre enfoques exploratorios y confirmatorios, y entre modelos de medición y relacionales.
- Repasar conceptos estadísticos clave: varianza, covarianza, correlación (Pearson y brevemente poli/tetracórica).
- Revisitar la regresión lineal múltiple (RLM), enfatizando el control estadístico y la interpretación de coeficientes estandarizados.
- Comprender la lógica de la inferencia estadística en regresión (test de hipótesis sobre coeficientes) y su importancia (y limitación con
lm) en diseños complejos.
Parte I: El Mundo de los Modelos Multivariados
¿Por Qué Modelos Multivariados?
La realidad social es compleja. Los fenómenos que estudiamos (desigualdad, movilidad social, opinión pública, comportamiento electoral…) raramente dependen de una sola causa.
- Análisis Bivariado (Correlación, t-test, Chi²): Útil para explorar relaciones iniciales entre dos variables, pero limitado. No captura la red de influencias simultáneas.
- Modelos Multivariados: Son nuestra herramienta para representar y analizar sistemas con múltiples variables interactuando. Nos permiten:
- Describir relaciones complejas.
- Explicar fenómenos considerando múltiples factores y controlando por variables alternativas.
- Predecir resultados con mayor precisión.
- Testear teorías sociológicas que postulan relaciones múltiples.
Funciones de los Modelos en Cs. Sociales
Los modelos multivariados nos sirven para:
- Formalizar Teorías: Traducir ideas teóricas verbales a relaciones específicas entre variables, permitiendo rigurosidad y testeo empírico.
- Identificar Efectos Netos: Aislar el impacto de una variable de interés sobre otra, eliminando estadísticamente la influencia de terceras variables (control estadístico). ¿Cuál es el efecto “puro” de la educación sobre el ingreso, una vez que consideramos la experiencia laboral y el origen socioeconómico?
- Descubrir Estructuras Subyacentes: Encontrar patrones ocultos o dimensiones latentes en conjuntos grandes de variables (Ej: ¿Qué dimensiones básicas explican las respuestas a una batería de preguntas sobre actitudes políticas?).
- Evaluar Ajuste Teoría-Datos: Determinar si un modelo teórico propuesto es compatible con los datos observados.
Un Mapa para Navegar los Modelos
Podemos organizar los modelos que veremos en el curso (y otros) según dos ejes principales:
Eje 1: ¿Exploramos o Confirmamos?
- Modelos Exploratorios: ¿Qué nos dicen los datos? Buscamos patrones sin una hipótesis fuerte a priori.
- Modelos Confirmatorios: ¿Se ajustan los datos a mi teoría? Testeamos una estructura hipotetizada previamente.
Eje 2: ¿Medimos Conceptos o Relacionamos Variables?
- Modelos de Medición: ¿Cómo se relacionan los indicadores observables con un concepto latente?
- Modelos Relacionales (o Estructurales): ¿Cómo se relacionan distintas variables (observadas o latentes) entre sí?
Eje 1: Exploratorio vs. Confirmatorio
- Análisis Factorial Exploratorio (AFE):
- Objetivo: Identificar factores o dimensiones latentes comunes que explican las correlaciones entre un conjunto de variables observadas (ítems de una escala, indicadores).
- Pregunta: ¿Cuántas dimensiones subyacen a estos 20 ítems sobre bienestar? ¿Qué ítems cargan en qué dimensión?
- Guiado por los datos, busca descubrir estructura.
Eje 1: Exploratorio vs. Confirmatorio
- Análisis Factorial Confirmatorio (AFC), Análisis de Senderos, Modelos de Ecuaciones Estructurales (SEM):
- Objetivo: Testear si una estructura de relaciones (entre ítems y factores, o entre diferentes factores/variables) definida previamente por la teoría se ajusta bien a los datos observados.
- Pregunta: ¿Confirman los datos que la “autoeficacia” (medida por 4 ítems) predice el “rendimiento académico” (medido por notas), controlando por “apoyo familiar” (medido por 3 ítems)?
- Guiado por la teoría, busca validar un modelo específico.
Eje 2: Medición vs. Relacional
- Modelos de Medición:
- Se enfocan en la calidad de la medición. ¿Son fiables y válidos nuestros indicadores para medir el concepto abstracto que nos interesa?
- Central en AFE (¿qué miden los factores?) y AFC (¿miden bien los ítems el factor que creemos que miden?).
- Modelos Relacionales / Estructurales:
- Se enfocan en las relaciones entre variables (sean observadas o latentes).
- Regresión Lineal Múltiple (RLM): Relaciona variables observadas.
- Análisis de Senderos: Modela relaciones más complejas hipotetizadas entre variables observadas.
- Modelos de Ecuaciones Estructurales (SEM): El más general. Modela relaciones entre variables latentes y/o observadas, combinando modelos de medición y modelos relacionales.
(Estos ejes no son excluyentes, SEM por ejemplo, incluye ambos tipos de modelos).
Parte II: Repaso de Conceptos Estadísticos Clave
Variabilidad y Dispersión
Para entender relaciones, primero necesitamos entender cómo varían las variables por sí solas.
- Varianza (\(s^2\)): Promedio de las distancias al cuadrado de cada dato respecto a la media. Mide la dispersión total, pero en unidades al cuadrado (difícil interpretación directa). \[ s^2 = \frac{\sum (x_i - \bar{x})^2}{n-1} \]
- Desviación Estándar (\(s\)): Raíz cuadrada de la varianza. Vuelve a las unidades originales de la variable. Es la medida de dispersión más usada e interpretable. \[ s = \sqrt{s^2} \]
Mayor \(s\) -> Mayor heterogeneidad / dispersión.
Variabilidad y Dispersión
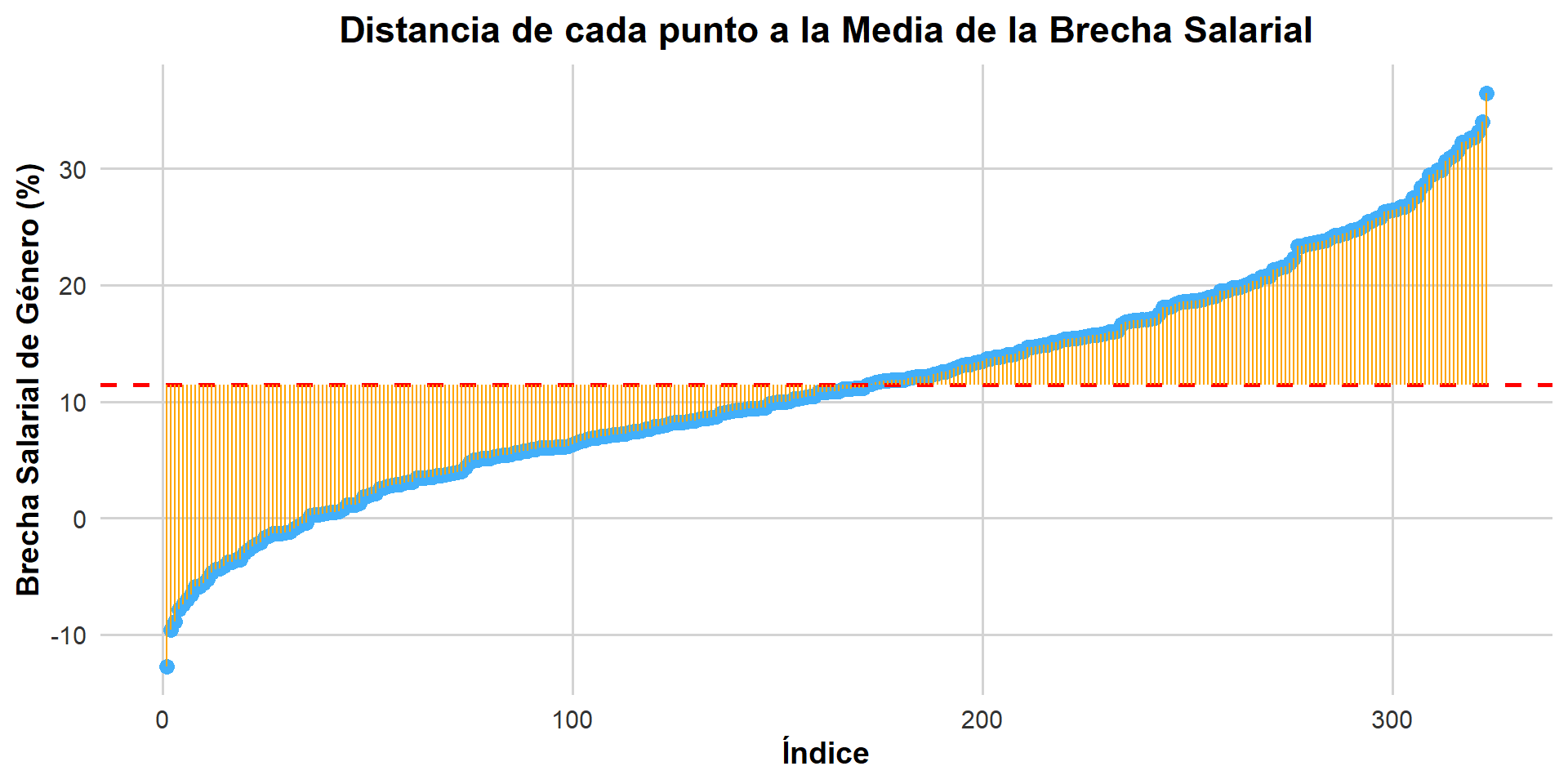
Co-Variación: Covarianza y Correlación
¿Cómo varían dos variables juntas?
- Covarianza: Mide la dirección de la relación lineal entre dos variables. \[ Cov(x,y) = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{n-1} \]
- Signo (+): Relación directa (si X sube, Y tiende a subir).
- Signo (-): Relación inversa (si X sube, Y tiende a bajar).
- Problema: Su magnitud depende de las escalas de X e Y. No permite comparar fuerza de asociación entre distintos pares de variables.
Co-Variación: Covarianza y Correlación
- Correlación de Pearson (r): La covarianza estandarizada. \[ r = \frac{Cov(x,y)}{s_x s_y} \]
- Varía entre -1 y +1.
- +1: Correlación lineal positiva perfecta.
- -1: Correlación lineal negativa perfecta.
- 0: Ausencia de correlación lineal.
- Ventaja: Adimensional, permite comparar la fuerza de la relación lineal.
- Limitación Central: Sólo mide relaciones LINEALES. Una correlación de 0 no significa que no haya ninguna relación (podría ser curvilínea).
Graficos de dispersión y correlación
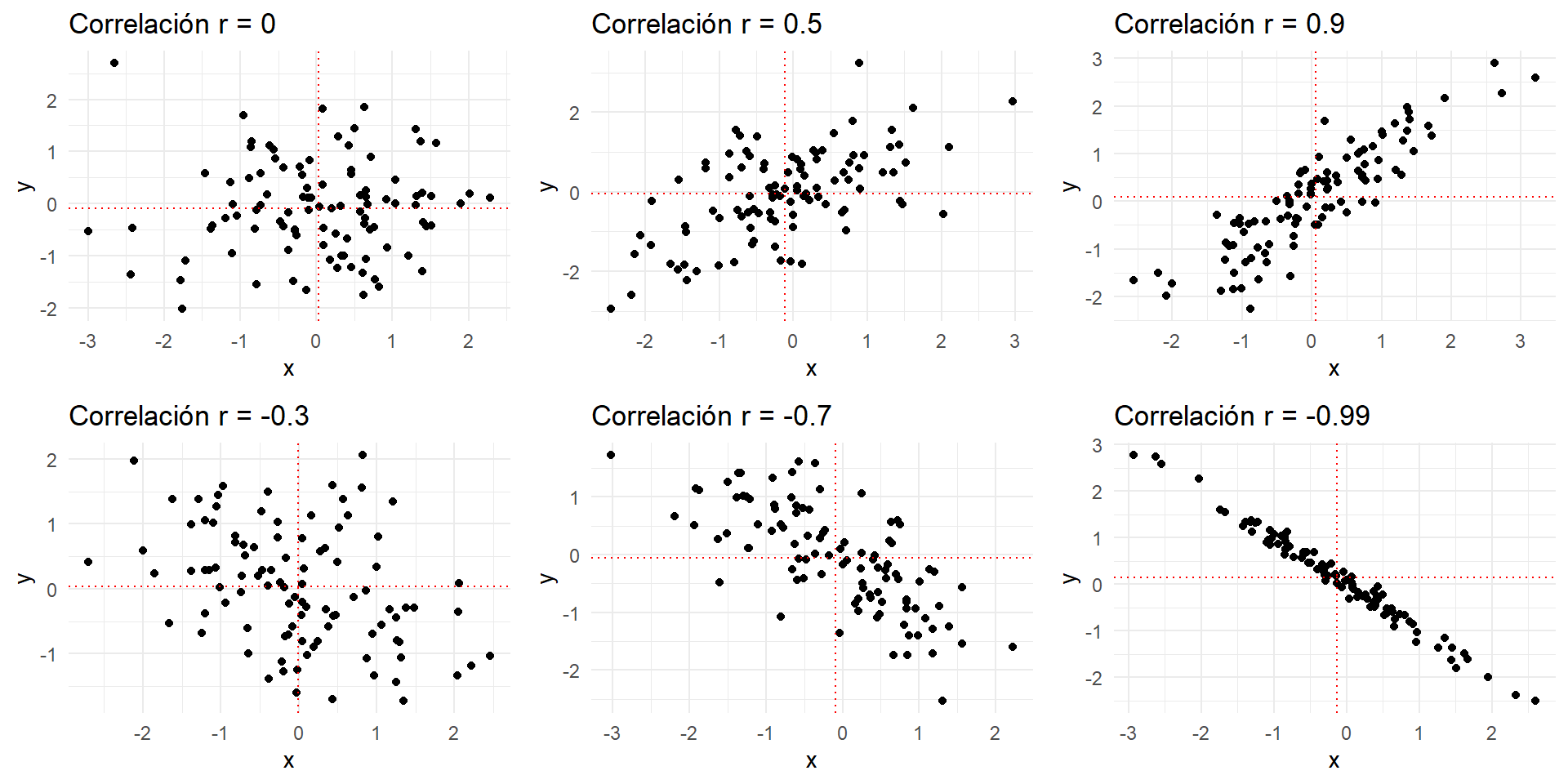
Correlaciones para Datos No Continuos
¿Qué hacemos si nuestras variables son ordinales (ej. escalas Likert: “Muy en desacuerdo” a “Muy de acuerdo”) o dicotómicas (ej. Sí/No, Hombre/Mujer)? Pearson no es ideal.
Idea Clave: Suponer que detrás de la variable categórica observada existe una variable latente continua (no observable) que sigue una distribución normal. Lo que observamos son “cortes” en esa distribución latente.
- Correlación Policórica: Estima la correlación entre las variables latentes continuas asumidas detrás de dos variables ordinales.
- Correlación Tetracórica: Estima la correlación entre las variables latentes continuas asumidas detrás de dos variables dicotómicas.
Correlaciones para Datos No Continuos
¿Por qué son importantes?
* El Análisis Factorial (AFE/AFC) se basa en analizar la matriz de correlaciones entre las variables.
* Si tenemos variables ordinales o dicotómicas, usar la matriz de correlaciones de Pearson puede distorsionar los resultados del AFE/AFC. Es más adecuado usar una matriz de correlaciones policóricas/tetracóricas (o mixtas).
(En R, el paquete polycor permite calcularlas).
Parte III: De la Correlación a la Regresión Lineal
Más Allá de la Asociación: Regresión Lineal Simple (RLS)
La correlación nos dice si y cómo X e Y varían juntas linealmente. La Regresión Lineal Simple va un paso más allá: intenta modelar esa relación y predecir el valor de la variable dependiente (Y) a partir de la variable independiente (X) usando una línea recta.
Ecuación de la Recta de Regresión: \[ \hat{y} = a + bx \]
- \(\hat{y}\): Es el valor de Y predicho por el modelo para un valor dado de X.
- \(a\): Es el intercepto (o constante). Representa el valor predicho de Y cuando X es igual a 0. Su interpretación práctica depende de si X=0 tiene sentido en el contexto del problema.
- \(b\): Es la pendiente (o coeficiente de regresión). Indica el cambio promedio estimado en Y por cada incremento de una unidad en X. Es la medida clave del efecto de X sobre Y en este modelo.
Visualizando la RLS
La recta de regresión busca ser la línea que “mejor representa” la tendencia lineal en la nube de puntos de un diagrama de dispersión. La recta resume la relación lineal promedio.
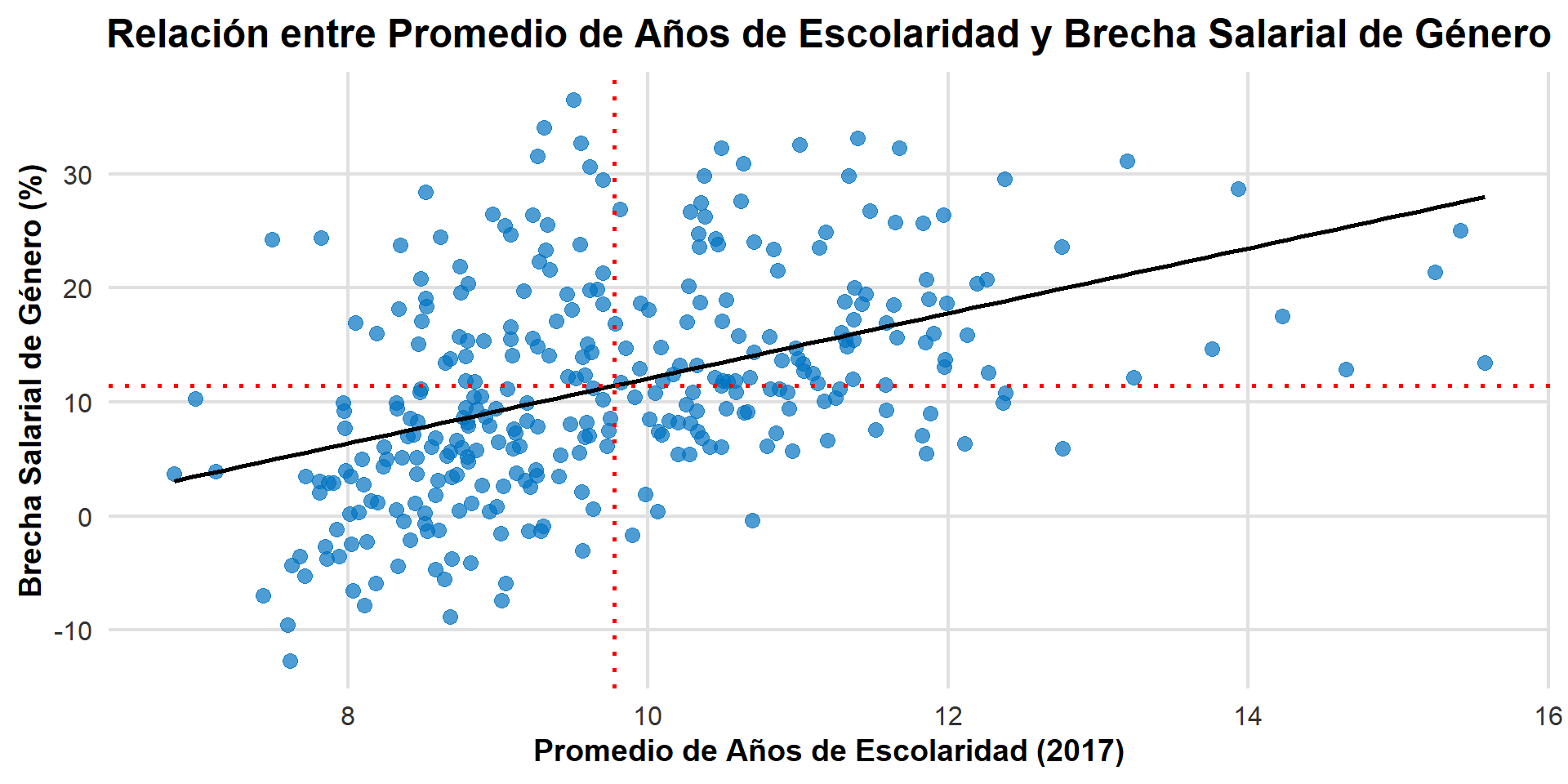
¿Cómo Encontrar la “Mejor” Recta? Mínimos Cuadrados (OLS)
Hay infinitas rectas posibles. OLS (Ordinary Least Squares) es el método estándar para elegir la “mejor”:
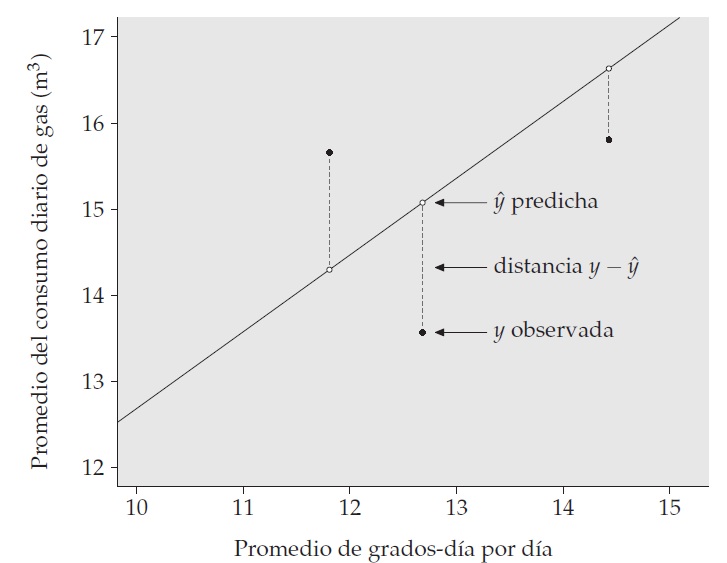
- Residuo (\(e_i\)): Para cada punto (\(x_i, y_i\)), es la diferencia vertical entre el valor observado \(y_i\) y el valor predicho por la recta \(\hat{y}_i\). \[ e_i = y_i - \hat{y}_i = y_i - (a + bx_i) \]
- El residuo es el error de predicción del modelo para esa observación.
- OLS busca la recta (los valores de \(a\) y \(b\)) que minimiza la SUMA de los CUADRADOS de todos los residuos: \[ \text{Minimizar } \sum e_i^2 = \sum (y_i - \hat{y}_i)^2 \]
Visualización de la distancia entre la recta y los casos
Fórmulas para OLS (RLS)
Para calcular la pendiente 𝑏y la ordenada en el origen 𝑎, se utilizan las siguientes fórmulas: \[ b = r \frac{s_y}{s_x} \]
\[ a = \bar{y} - b \bar{x} \] Donde:
\(r\) es la correlación entre \(x\) y \(y\).
\(s_x\) y \(s_y\) son las desviaciones estándar de \(x\) y \(y\).
\(\bar{x}\) y \(\bar{y}\) son las medias de \(x\) y \(y\), respectivamente.
Análisis de Residuos: Evaluando el Ajuste del Modelo
Una vez ajustada la recta, analizar los residuos es crucial para ver si el modelo lineal es apropiado.
- Gráfico de Residuos: Se grafica cada residuo (\(e_i\)) contra el valor predicho correspondiente (\(\hat{y}_i\)).
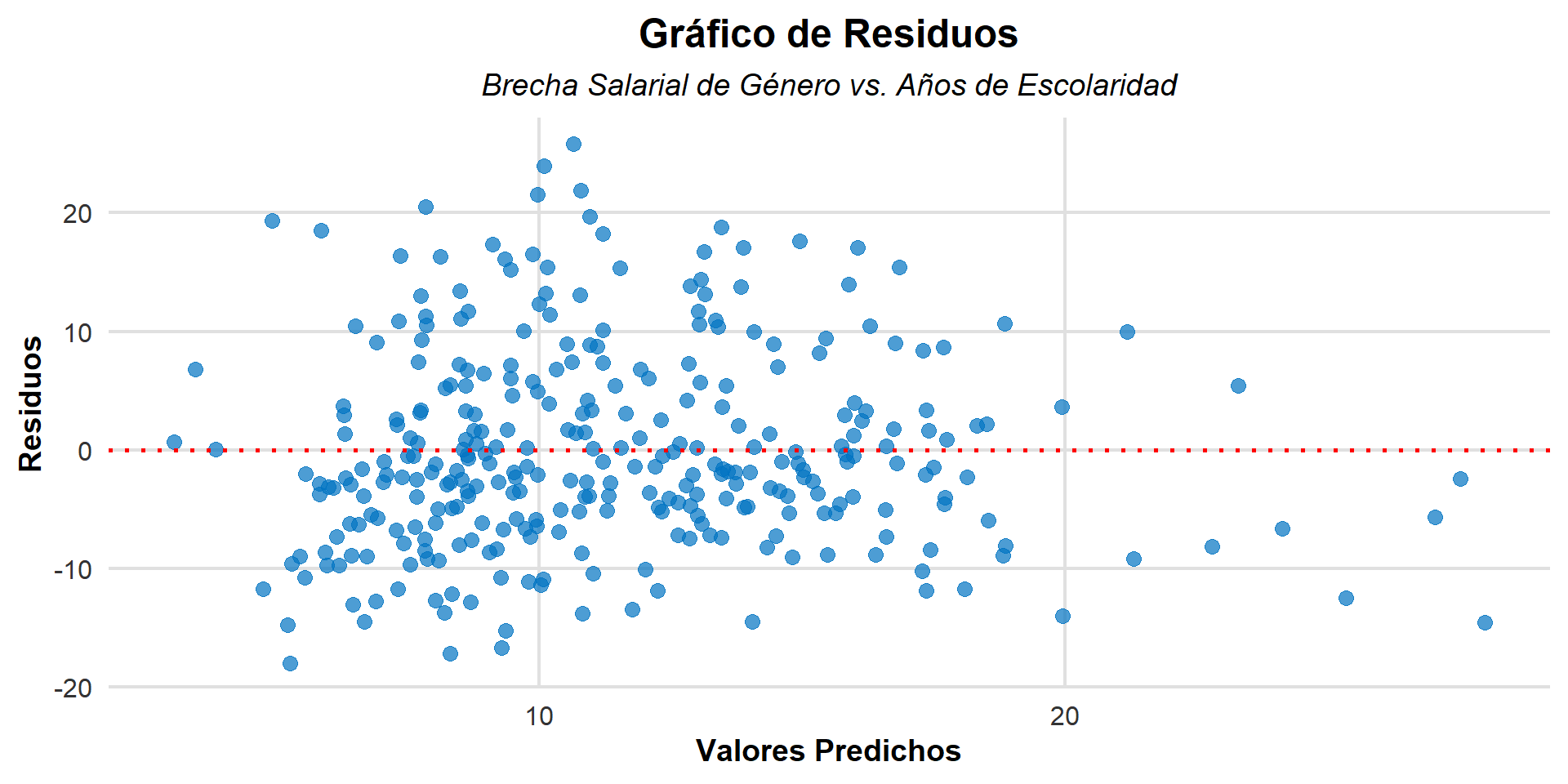
Interpretando el Gráfico de Residuos
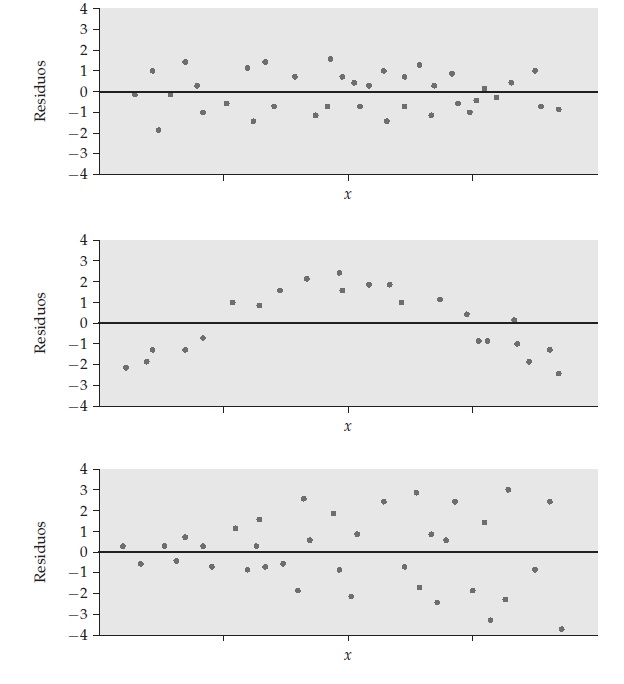
¿Qué buscamos en el gráfico de residuos vs. predichos?
Ideal (Buen Ajuste): Una nube de puntos dispersa aleatoriamente alrededor de la línea horizontal en 0, sin patrones claros. Esto indica homocedasticidad (la varianza del error es constante).
Problemas (Mal Ajuste Lineal):
- Patrón Curvo: Sugiere que la relación entre X e Y no es lineal. Un modelo lineal no es adecuado.
- Forma de Embudo (Heterocedasticidad): La dispersión de los residuos aumenta (o disminuye) a medida que aumentan los valores predichos. Viola el supuesto de varianza constante del error. Las predicciones son menos fiables para ciertos rangos de Y.
Diagramas de residuos
Bondad de Ajuste: Coeficiente de Determinación (\(R^2\))
¿Qué proporción de la variabilidad total de Y es “explicada” por nuestra recta de regresión basada en X?
- Descomposición de la Varianza: La varianza total de Y (SST - Sum of Squares Total) se puede descomponer en:
- Varianza Explicada por la Regresión (SSR - Sum of Squares Regression).
- Varianza No Explicada o Residual (SSE - Sum of Squares Error). \[ SST = SSR + SSE \] \[ \sum(y_i - \bar{y})^2 = \sum(\hat{y}_i - \bar{y})^2 + \sum(y_i - \hat{y}_i)^2 \]
Bondad de Ajuste: Coeficiente de Determinación (\(R^2\))
- \(R^2\): Es la proporción de la varianza total que es explicada por el modelo. \[ R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST} \]
- Varía entre 0 y 1. Un \(R^2\) de 0.13 indica que el 13% de la varianza en Y está asociada linealmente con X.
Limitaciones de RLS y la Necesidad de RLM
La Regresión Lineal Simple es un buen punto de partida, pero asume que solo X influye en Y (o que otros factores no están correlacionados con X). En ciencias sociales, esto es raramente cierto.
Problema Central: El coeficiente \(b\) de RLS puede capturar no solo el efecto de X, sino también efectos espurios o confundidos por otras variables omitidas (\(Z_1, Z_2, ...\)).
Ejemplo Clásico: Número de bomberos en un incendio (X) y daños causados (Y). RLS mostrará una correlación positiva (\(b>0\)). ¿Significa que los bomberos causan daño? No, la variable omitida es la magnitud del incendio (Z), que afecta a ambos.
Necesitamos incluir múltiples predictores para controlar estos efectos.
Regresión Lineal Múltiple (RLM): El Poder del Control
RLM: Modela Y en función de varios predictores (\(X_1, X_2, ..., X_k\)) simultáneamente.
\[ Y = b_0 + b_1 X_1 + b_2 X_2 + ... + b_k X_k + \epsilon \]
Concepto Clave: Control Estadístico
* La RLM nos permite estimar el efecto de \(X_1\) sobre Y, como si mantuviéramos constantes los valores de \(X_2, ..., X_k\).
* Es un ajuste matemático para aislar la asociación única de cada predictor con Y, eliminando la influencia compartida (correlación) entre los predictores.
* Fundamental en estudios observacionales (como encuestas) donde no podemos hacer asignación aleatoria experimental.
Interpretando Coeficientes Parciales en RLM (\(b_j\))
El \(b_j\) en RLM es un coeficiente de regresión parcial. Su interpretación SIEMPRE incluye la cláusula “controlando por las demás variables”:
- \(b_j\) representa el cambio promedio estimado en Y por cada unidad de aumento en \(X_j\), manteniendo constantes todas las demás variables X incluidas en el modelo.
Ejemplo: Ingreso = b_0 + b_1 Escolaridad (años) + b_2 Edad (años)$.
* \(b_1 = 88000\): Por cada año adicional de escolaridad, el ingreso aumenta en promedio $88.000, para personas de la misma edad.
* \(b_2 = 7600\): Por cada año adicional de edad, el ingreso aumenta en promedio $7600, para personas con la misma escolaridad.
Diferencia con RLS: El efecto ahora es “neto” de la influencia de las otras variables en el modelo.
Predictores Categóricos en RLM: Variables Dummy
¿Cómo incluir variables como “Sexo” o “Nivel Educativo”?
- Dicotómicas (0/1): (Ej: Mujer=0, Hombre=1)
- Se incluyen directamente.
- El \(b\) asociado es la diferencia promedio en Y entre el grupo 1 (Hombre) y el grupo 0 (Mujer, la referencia), controlando por las otras X.
Predictores Categóricos en RLM: Variables Dummy
- Politómicas (k categorías): (Ej: Nivel Ed: Básico/Medio/Superior)
- Se crean k-1 variables dummy. Una categoría se deja como referencia (Ej: Básico).
- Dummy Medio: 1 si Ed=Media, 0 si no.
- Dummy Superior: 1 si Ed=Superior, 0 si no.
- El modelo sería: \(Y = b_0 + ... + b_{medio} \times Dummy_{Medio} + b_{superior} \times Dummy_{Superior}\)
- \(b_{medio}\): Diferencia promedio en Y entre Ed. Media y Ed. Básica (ref.), controlando por otras X.
- \(b_{superior}\): Diferencia promedio en Y entre Ed. Superior y Ed. Básica (ref.), controlando por otras X.
(R con factor() lo hace automáticamente, eligiendo una referencia).
Comparando Efectos: Coeficientes Estandarizados (β)
Los \(b_j\) dependen de las unidades. ¿Cómo comparar si un año más de edad tiene un impacto “más fuerte” en el ingreso que un año más de escolaridad?
Coeficientes Beta Estandarizados (β):
* Se obtienen estandarizando todas las variables (Y y Xs) a \(Z\)-scores (media 0, DE 1) antes de la regresión.
* Interpretación: Indican cuántas Desviaciones Estándar (DE) cambia Y por cada una DE de cambio en \(X_j\), controlando por las otras Xs (en DE).
* Ventaja: Adimensionales. Permiten comparar la magnitud relativa del efecto de predictores con diferentes unidades. Un \(\beta\) de 0.30 tiene un impacto relativo mayor que un \(\beta\) de 0.15.
* Usos: Identificar predictores más influyentes, comparar resultados entre estudios, base para Senderos y SEM.
Ajuste del Modelo RLM: \(R^2\) y \(R^2\) Ajustado
- \(R^2\) Múltiple:
- Proporción de varianza de Y explicada por TODOS los predictores \(X_1, ..., X_k\) juntos.
- Igual interpretación (0 a 1), pero ahora refleja el poder explicativo conjunto.
- Problema: Se infla al añadir variables, incluso si son irrelevantes.
- \(R^2\) Ajustado:
- Corrige el \(R^2\) considerando el número de predictores (k) y el tamaño muestral (n).
- \[ R^2_{ajustado} = 1 - \left( \frac{(1 - R^2)(n - 1)}{n - k - 1} \right) \]
- Penaliza por complejidad innecesaria. Mejor para comparar modelos con diferente número de predictores.
Parte IV: Inferencia en Regresión
Inferencia: De la Muestra a la Población
Los \(b_j\) son estimaciones muestrales de los parámetros poblacionales \(\beta_j\). Debido al error muestral, si tomáramos otra muestra, obtendríamos \(b_j\) ligeramente diferentes.
Pregunta Central: ¿El efecto \(b_j\) que vemos en nuestra muestra es “real” (estadísticamente significativo) en la población, o podría ser solo ruido muestral? ¿Es \(\beta_j\) (el efecto poblacional) diferente de cero, controlando por los demás?
Test de Hipótesis para Coeficientes (\(b_j\))
Para cada \(b_j\) (usualmente excluyendo \(b_0\)):
- \(H_0: \beta_j = 0\) (No hay efecto parcial de \(X_j\) en la población).
- \(H_1: \beta_j \neq 0\) (Sí hay efecto parcial de \(X_j\) en la población).
Herramientas de Inferencia:
1. Error Estándar del Coeficiente (\(SE(b_j)\)): Mide la precisión de la estimación \(b_j\). Un SE pequeño indica más confianza.
2. Estadístico t: \(t = b_j / SE(b_j)\). ¿Cuántos SEs se aleja \(b_j\) de 0?
3. p-valor: Probabilidad de observar un \(|t|\) tan grande o más, si \(H_0\) fuera cierta.
Interpretación y Decisión
Interpretación del p-valor:
* Un p-valor pequeño (ej. < 0.05) significa que es muy improbable observar un efecto tan grande como \(b_j\) si realmente no hubiera efecto en la población (\(\beta_j = 0\)).
Regla de Decisión (Nivel \(\alpha = 0.05\)):
* Si p-valor < 0.05:
* Rechazamos \(H_0\).
* Concluimos que el efecto de \(X_j\) es estadísticamente significativo. Hay evidencia para afirmar que \(\beta_j\) es distinto de cero.
* Si p-valor ≥ 0.05:
* No rechazamos \(H_0\).
* No hay evidencia suficiente para afirmar que \(\beta_j\) sea distinto de cero. No significa que sea exactamente cero, solo que no podemos descartarlo.
Inferencia con muestras complejas
Todo lo anterior sobre inferencia (SE, t, p-valores) calculado con lm() en R asume Muestreo Aleatorio Simple.
SI TUS DATOS SON DE UNA ENCUESTA COMPLEJA (CASEN):
lm()ignora los estratos, conglomerados y pesos.- Los SE estarán incorrectos (generalmente subestimados).
- Los p-valores estarán incorrectos (generalmente subestimados).
- Esto puede llevar a conclusiones falsas sobre la significacia
Solución: * Usar el objeto de diseño (survey::svydesign o srvyr::as_survey). * Usar survey::svyglm() en lugar de lm() o glm(). * svyglm SÍ calcula los SE y p-valores correctamente, considerando el diseño.
Próximos Pasos: El Práctico
En el práctico repasaremos en R con lm():
- Correlaciones.
- RLS y RLM con predictores continuos y categóricos.
- Interpretación de coeficientes crudos y estandarizados.
- Interpretación de la salida de
summary(lm()), incluyendo p-valores… - Cálculo de regresiones usando muestras complejas.
