Análisis Factorial Exploratorio (AFE)
Sesión 7: Descubriendo Dimensiones Latentes
2025-05-12
Objetivos de la Sesión
En esta primera parte sobre Análisis Factorial Exploratorio (AFE), nos enfocaremos en:
- Comprender qué son las variables latentes y por qué son cruciales en Ciencias Sociales.
- Definir el Análisis Factorial Exploratorio (AFE): sus objetivos y lógica fundamental.
- Diferenciar brevemente AFE del Análisis de Componentes Principales (ACP).
- Detallar las etapas clave del proceso de AFE.
- Profundizar en la preparación de los datos y la evaluación de supuestos necesarios para un AFE robusto.
- Entender cómo se extraen los factores iniciales y se interpreta la matriz factorial.
Variables Latentes en Sociología
Muchos conceptos centrales en sociología no son directamente observables ni medibles con una sola pregunta.
- Ejemplos: Autoritarismo, Anomia, Capital Cultural, Bienestar Subjetivo, Alienación, Conciencia de Clase…
Estos son CONCEPTOS ABSTRACTOS o CONSTRUCTOS TEÓRICOS.
En estadística, los llamamos VARIABLES LATENTES:
- No se miden directamente.
- Se infieren a partir de un conjunto de variables observadas (indicadores) que creemos que reflejan o son causadas por esa variable latente.
El Rol del AFE
Si una variable latente (ej. “Satisfacción Laboral”) no es visible, ¿cómo la estudiamos?
- Diseñamos múltiples preguntas (ítems o indicadores) que intentan capturar diferentes facetas de ese concepto.
- “¿Está ud. satisfecho con su salario?”
- “¿Siente que su trabajo es reconocido?”
- “¿Tiene buenas relaciones con sus colegas?”
- Aplicamos estas preguntas a una muestra.
- Análisis Factorial Exploratorio (AFE): Una técnica estadística que nos ayuda a determinar si las respuestas a estos ítems se agrupan de manera coherente, sugiriendo que están midiendo una (o varias) dimensiones subyacentes (los factores latentes).
Análisis Factorial Exploratorio (AFE)?
El AFE es un conjunto de técnicas estadísticas multivariadas cuyo objetivo principal es:
Reducir la dimensionalidad de un conjunto de p variables observadas (correlacionadas entre sí) a un número menor de k factores latentes no observados (factores comunes), con la menor pérdida de información posible.
En esencia: Busca identificar la estructura subyacente en las relaciones (correlaciones) entre las variables observadas.
- Si varias variables están altamente correlacionadas entre sí, es probable que estén midiendo un mismo concepto o factor latente.
- El AFE intenta descubrir estos “grupos” de variables y los factores que representan.
Objetivos Específicos del AFE
- Analizar la Estructura de Correlaciones:
- Determinar si las variables observadas comparten suficiente varianza común como para justificar la existencia de factores latentes.
- Identificar cuántos factores latentes son necesarios para explicar adecuadamente las correlaciones observadas.
- Identificar el Significado de los Factores:
- Interpretar qué representa cada factor latente, examinando qué variables observadas “cargan” o se asocian fuertemente con él.
- Obtener Puntuaciones Factoriales (Factor Scores):
- Calcular un valor estimado para cada individuo en cada uno de los factores latentes identificados.
- Estas puntuaciones pueden usarse luego como variables en otros análisis (regresión, ANOVA, etc.), representando de forma sintética las dimensiones encontradas.
El Modelo Matemático del AFE (Conceptual)
La idea básica es que cada variable observada (\(X_i\)) puede ser expresada como una combinación lineal de:
- Un conjunto de factores comunes (\(F_1, F_2, ..., F_k\)) que son compartidos por múltiples variables observadas.
- Un factor único (\(e_i\)) que es específico para esa variable \(X_i\) y representa la parte de su varianza que no es compartida con otros ítems (error de medida + varianza específica).
\[ X_1 = \lambda_{11}F_1 + \lambda_{12}F_2 + ... + \lambda_{1k}F_k + e_1 \] \[ X_2 = \lambda_{21}F_1 + \lambda_{22}F_2 + ... + \lambda_{2k}F_k + e_2 \] \[ ... \] \[ X_p = \lambda_{p1}F_1 + \lambda_{p2}F_2 + ... + \lambda_{pk}F_k + e_p \]
- \(\lambda_{ij}\) (lambda): Es la carga factorial de la variable \(X_i\) en el factor \(F_j\). Indica la fuerza y dirección de la relación entre el ítem y el factor.
AFE vs. Análisis de Componentes Principales (ACP)
Son técnicas similares (ambas buscan reducir dimensiones) pero conceptualmente diferentes:
- Análisis de Componentes Principales (ACP):
- Objetivo: Crear un conjunto más pequeño de variables (componentes) que capturen la máxima varianza total posible de las variables originales.
- Asume que toda la varianza de cada variable es “común” (no distingue varianza común de única/error).
- Los componentes son combinaciones lineales de las variables observadas.
- Es más una técnica de transformación y resumen de datos.
AFE vs. Análisis de Componentes Principales (ACP)
- Análisis Factorial Exploratorio (AFE) (específicamente de Factor Común):
- Objetivo: Identificar factores latentes que expliquen las correlaciones (varianza común) entre las variables observadas.
- Asume un modelo donde la varianza de cada variable se divide en varianza común (comunalidad) y varianza única.
- Los factores latentes se postulan como “causas” de las variables observadas.
- Es más una técnica de modelado de la estructura subyacente.
En la práctica: A menudo dan resultados similares, especialmente con muchas variables y altas comunalidades. ACP se usa a veces como un método de extracción en AFE.
Etapas del Análisis Factorial Exploratorio
El proceso de AFE suele seguir una serie de pasos definidos:
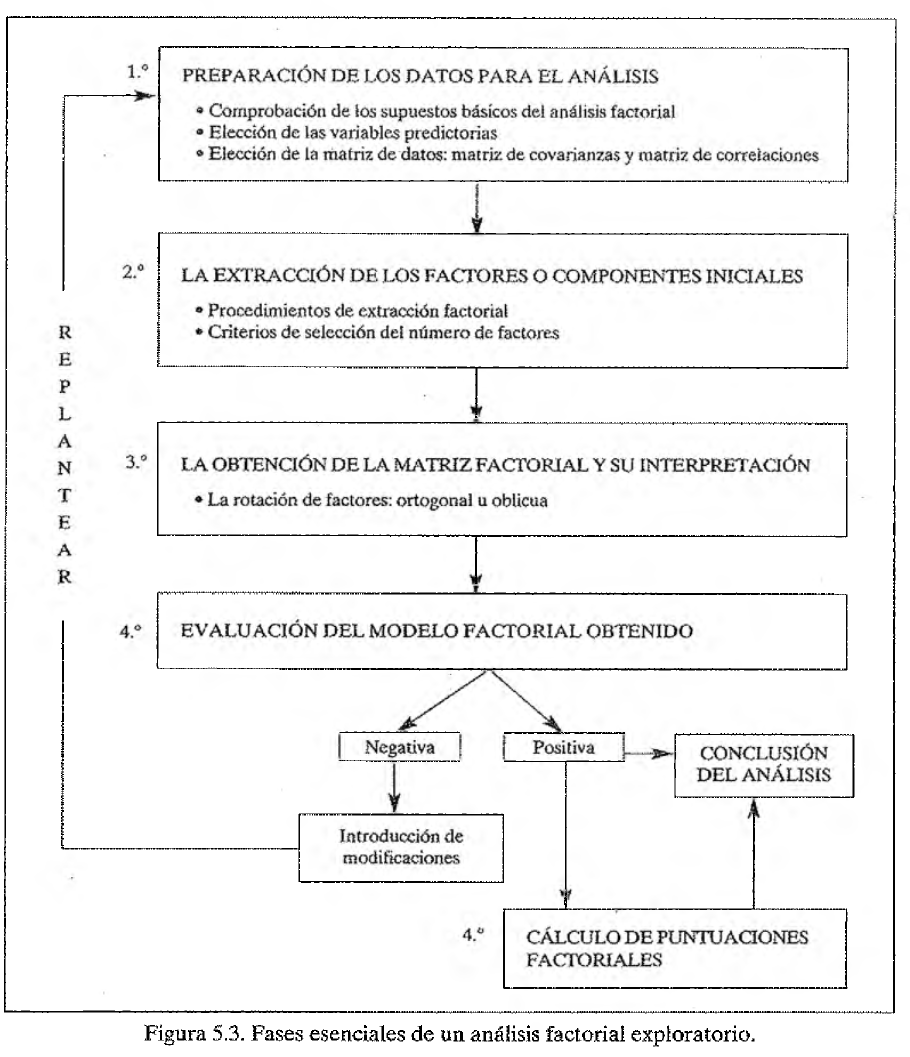
Preparación de Datos y Supuestos
Antes de Empezar: Chequeos Esenciales
Como toda técnica estadística, el AFE tiene requisitos y supuestos sobre los datos:
- Nivel de Medición de las Variables.
- Tamaño Muestral Adecuado.
- Colinealidad (¡Necesaria!) y Ausencia de Multicolinealidad Extrema.
- (Idealmente) Normalidad Multivariante.
- Tratamiento de Casos Perdidos y Atípicos.
- Estandarización (Opcional pero Recomendada).
1. Nivel de Medición
- Tradicionalmente, el AFE se desarrolló para variables continuas (intervalares o de razón).
- Sin embargo, es muy común usarlo con variables ordinales (ej. escalas Likert).
- Si son ordinales: Es crucial usar la matriz de correlaciones adecuada.
- Si las variables ordinales tienen pocas categorías (ej. < 5-7) o distribuciones muy asimétricas, la correlación de Pearson puede subestimar la verdadera asociación.
- En estos casos, se prefiere una matriz de correlaciones POLICÓRICAS.
- Si son dicotómicas, se usarían correlaciones TETRACÓRICAS.
- Si son ordinales: Es crucial usar la matriz de correlaciones adecuada.
1. Nivel de Medición
2. Tamaño Muestral
No hay reglas únicas, pero sí recomendaciones generales:
- Mínimo Absoluto: Al menos 5 casos por cada variable incluida en el análisis. Es mejor si son 10-20 casos por variable.
- Tamaño Total Mínimo: Generalmente se recomienda un N > 100. Idealmente N > 200 o 300 para obtener soluciones factoriales más estables.
- Relación con Comunalidades y Número de Factores:
- Si las comunalidades (proporción de varianza de un ítem explicada por los factores) son altas (ej. > 0.6-0.7) y hay pocos factores bien definidos, se pueden obtener resultados estables con muestras más pequeñas (ej. N=100-150).
- Si las comunalidades son bajas y/o se esperan muchos factores o factores débiles, se necesitan muestras más grandes.
- ¡Considerar Casos Perdidos y Atípicos! El N efectivo puede disminuir después de la limpieza de datos.
3. Colinealidad
A diferencia de la regresión donde la multicolinealidad es un problema, en AFE necesitamos que las variables estén correlacionadas.
- Lógica: Si las variables no se correlacionan entre sí, no pueden estar compartiendo varianza común, y por lo tanto, no habrá factores latentes que las agrupen.
- Evaluación Inicial:
- Inspeccionar la matriz de correlaciones: Buscar correlaciones significativas (ej. |r| > 0.30). Si la mayoría son cercanas a cero, el AFE no es apropiado.
- Test de Esfericidad de Bartlett:
- H0: La matriz de correlaciones es una matriz identidad (variables no correlacionadas).
- H1: La matriz de correlaciones NO es una matriz identidad.
- Resultado deseado: Rechazar H0 (p-valor < 0.05). Indica que hay suficiente correlación para proceder.
- Precaución: Este test es sensible al tamaño muestral (con N grande, casi siempre es significativo) y asume normalidad multivariante.
3. Multicolinealidad: El Test KMO
Además de que haya correlación, necesitamos que esta correlación sea “factorizable”, es decir, que forme patrones que sugieran factores comunes.
- Medida de Adecuación Muestral de Kaiser-Meyer-Olkin (KMO):
- Compara la magnitud de las correlaciones observadas con la magnitud de las correlaciones parciales (correlación entre dos variables controlando el efecto de las demás).
- Si las correlaciones parciales son pequeñas, sugiere que la correlación entre pares de variables se debe a factores comunes subyacentes.
3. Multicolinealidad: El Test KMO
- Valores de KMO varían de 0 a 1. Se interpreta como:
* > 0.90: Excelente
* 0.80 - 0.89: Bueno * 0.70 - 0.79: Aceptable
* 0.60 - 0.69: Mediocre
* 0.50 - 0.59: Malo
* < 0.50: Inaceptable
- Se calcula un KMO global y KMOs individuales para cada variable (MSA - Measure of Sampling Adequacy). Variables con MSA bajo (<0.50) podrían ser candidatas a eliminarse del análisis.
El KMO es preferible al test de Bartlett si no se cumple la normalidad multivariante.
4. Normalidad Multivariante
- Idealmente: El AFE (especialmente con métodos de extracción como Máxima Verosimilitud - ML) asume normalidad multivariante (todas las variables y todas sus combinaciones lineales siguen una distribución normal).
- En la práctica: Es un supuesto difícil de cumplir estrictamente en ciencias sociales.
- Consecuencias de la No Normalidad:
- Puede afectar la precisión de los tests de significancia (ej. Test de Bartlett, tests de bondad de ajuste del modelo factorial).
- Puede sesgar la estimación de las cargas factoriales si se usa ML.
4. Normalidad Multivariante
- ¿Qué hacer?
- Evaluar normalidad univariada: Revisar asimetría y curtosis de cada variable. Valores de asimetría entre ± 2 (o ± 1) suelen considerarse aceptables.
- Si hay no normalidad severa:
- Considerar transformar variables (con cautela).
- Usar métodos de extracción más robustos a la no normalidad (ej. Mínimos Cuadrados Ordinarios (OLS), Ejes Principales (PAF), Mínimos Cuadrados No Ponderados (ULS)).
- Privilegiar KMO sobre Bartlett para evaluar factorabilidad.
5. Casos Perdidos y Atípicos
- Casos Perdidos (Missing Data):
- Evaluar: Proporción de NAs por variable y por caso. Patrón de missing (aleatorio o sistemático).
- Opciones (orden de preferencia general):
- Imputación Múltiple: Generalmente la mejor opción si los datos son MCAR o MAR.
- Estimación por Máxima Verosimilitud con Información Completa (FIML): Maneja NAs directamente en algunos software (no tan simple en AFE con R base).
- Imputación Simple (media, mediana, regresión): Puede sesgar varianzas y correlaciones. Usar con mucha cautela.
- Eliminación por lista (listwise deletion): Elimina cualquier caso con algún NA. Puede reducir drásticamente el N y sesgar si los NAs no son MCAR.
- Eliminación por pares (pairwise deletion): Calcula cada correlación usando todos los casos disponibles para ese par. Puede llevar a matrices de correlación no definidas positivas (problemático).
- Casos Atípicos (Outliers):
- Univariados: Valores extremos en una sola variable (Boxplots, Z-scores).
- Multivariados: Combinaciones inusuales de valores en múltiples variables. Se detectan con la Distancia de Mahalanobis (D2). Valores de D2 con p-valor < 0.001 suelen considerarse atípicos multivariantes.
- Impacto: Pueden distorsionar gravemente las correlaciones y, por ende, la solución factorial.
- Tratamiento: Investigar si son errores. Si son válidos pero extremos, considerar transformaciones, winsorización o eliminación (justificando).
6. Estandarización de Variables
- ¿Cuándo es relevante? Si las variables originales tienen escalas muy diferentes (ej. una va de 1 a 5, otra de 0 a 1000).
- Problema: Variables con mayor varianza pueden dominar la solución factorial si se usa la matriz de covarianzas.
- Solución Común: Trabajar con la matriz de correlaciones en lugar de la matriz de covarianzas. Esto es equivalente a estandarizar las variables (convertirlas a puntajes Z: media 0, DE 1) antes del análisis. \[ Z_i = \frac{X_i - \bar{X}}{s_X} \]
- La mayoría de los software de AFE usan la matriz de correlaciones por defecto, lo que implica una estandarización implícita.
- Ventaja: Todas las variables contribuyen de forma equitativa a la determinación de los factores, independientemente de su escala original.
Próximos Pasos
Una vez que los datos están preparados y se ha verificado la adecuación para el AFE:
- Elegir un Método de Extracción de Factores (ACP, Ejes Principales, Máxima Verosimilitud, etc.).
- Determinar el Número de Factores a Retener.
- (Si es necesario) Rotar la Solución Factorial para mejorar la interpretabilidad.
- Interpretar los Factores.
- Evaluar la Bondad de Ajuste del Modelo Factorial.
- (Opcional) Calcular Puntuaciones Factoriales.
