Análisis Factorial Exploratorio (AFE)
Sesión 8: Extracción, Rotación e Interpretación de Factores
2025-05-19
Objetivos de la Sesión
Continuando con nuestro estudio del Análisis Factorial Exploratorio (AFE):
- Revisar brevemente el proceso de selección de variables para AFE.
- Comprender los criterios para determinar el número de factores a extraer (Autovalores, Scree Plot, Análisis Paralelo).
- Conocer los principales métodos de extracción de factores (LSR/Mínimos Cuadrados, ML).
- Entender la necesidad y los tipos de rotación factorial (ortogonal vs. oblicua) para mejorar la interpretabilidad.
- Aprender a interpretar la matriz factorial (cargas factoriales) y nombrar los factores.
- Introducir la evaluación del modelo factorial y el uso de puntuaciones factoriales.
Recordatorio: Etapas del AFE
En la sesión anterior, nos enfocamos en la Preparación de Datos y Evaluación de Supuestos.
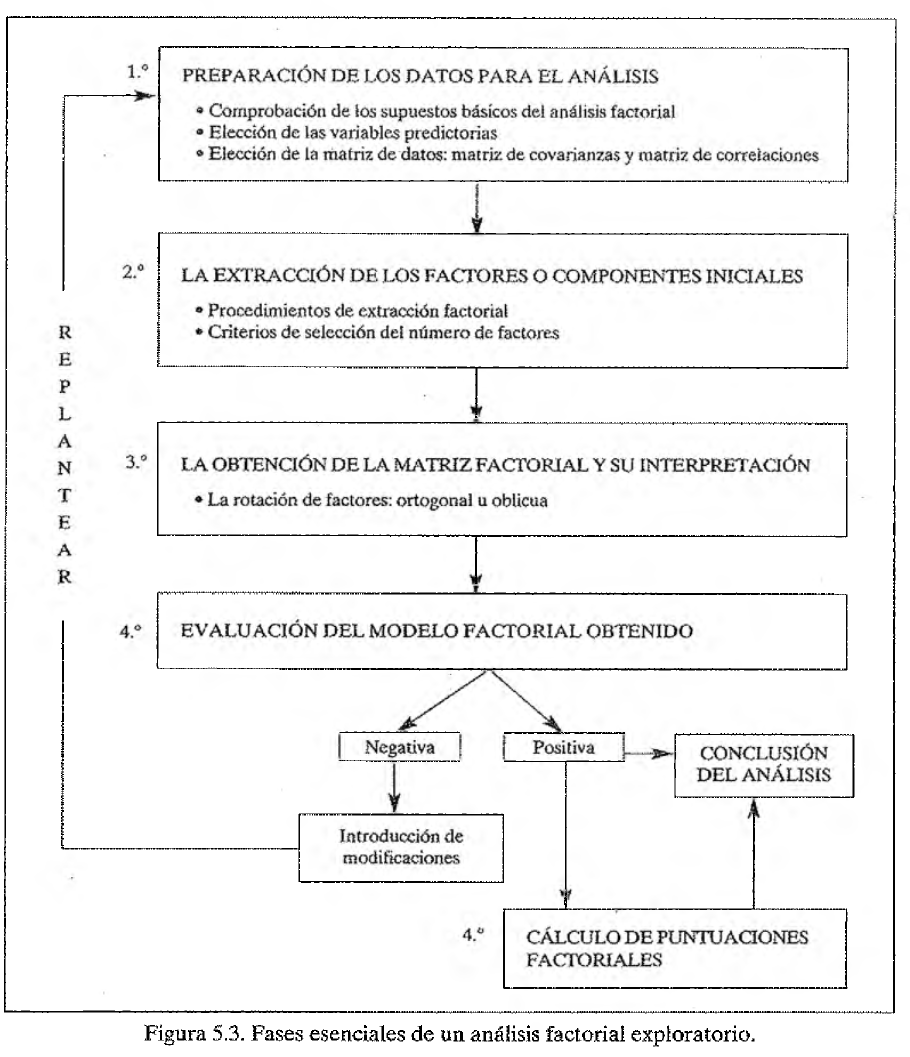
Hoy avanzamos hacia la Extracción e Interpretación de los Factores.
Extracción de Factores Comunes
1. Selección de Variables para el AFE
Antes de la extracción, la selección cuidadosa de las variables (ítems) es fundamental.
Consideraciones Clave:
- Relevancia Teórica:
- Las variables deben estar conceptualmente relacionadas con el/los constructo(s) latente(s) que se sospecha existen.
- ¿Qué dice la teoría o investigaciones previas sobre cómo se manifiesta este constructo?
- Calidad de las Variables:
- Nivel de medición adecuado (continuas u ordinales con suficientes categorías).
- Distribuciones razonables (evitar sesgos extremos si se usan métodos sensibles a la normalidad).
- Suficiente variabilidad (variables con poca o nula varianza no aportarán).
1. Selección de Variables para el AFE
- Factorabilidad (Recordatorio Sesión Anterior):
- Debe existir suficiente correlación entre las variables (KMO alto, Bartlett significativo si aplica).
- Variables con MSA (KMO individual) muy bajo (<0.50) podrían ser candidatas a ser eliminadas antes de la extracción.
2. Determinando el Número de Factores a Extraer
Este es uno de los pasos más críticos y subjetivos del AFE. Extraer muy pocos factores puede sobresimplificar la estructura; extraer demasiados puede llevar a factores poco sustantivos o difíciles de interpretar.
No hay una regla única, se usan múltiples criterios:
- Criterio de Kaiser (Autovalores > 1).
- Gráfico de Sedimentación (Scree Plot o Regla del Codo).
- Análisis Paralelo.
- Interpretabilidad Teórica y Sustantiva de la Solución.
(Los índices de ajuste como AIC, BIC, RMSEA son más propios de AFC o AFE con ML, pero pueden dar pistas).
Criterio de Kaiser (Autovalores > 1)
- Autovalor (Eigenvalue): Representa la cantidad de varianza total de todas las variables observadas que es explicada por un factor (o componente, si es ACP) específico.
- Si las variables están estandarizadas (media 0, DE 1), la varianza total de cada variable es 1. Un factor con autovalor > 1 explica más varianza que una variable original individual.
- Regla de Kaiser-Guttman: Retener solo los factores cuyo autovalor inicial (antes de la rotación) sea mayor que 1.
- Para AFE (Factor Común): Algunos autores sugieren retener factores con autovalor mayor que la varianza común promedio. Sin embargo, el >1 sobre la matriz de correlación original es el más común.
Ventaja: Simple y objetivo. Desventaja: Tiende a sobresestimar (extraer demasiados) o a veces subestimar el número de factores. Usar con precaución y junto a otros criterios.
Gráfico de Sedimentación (Scree Plot)
Es un método gráfico:
- Se ordenan los factores/componentes de mayor a menor autovalor.
- Se grafica el autovalor (eje Y) contra el número de factor (eje X).
- Se busca un “codo” (elbow) en el gráfico: un punto donde la pendiente de la línea que une los autovalores cambia bruscamente, aplanándose.
- Regla: Se retienen los factores que están antes del codo (los que están en la parte “empinada” de la curva). Estos representan la varianza sustantiva. Los factores después del codo se consideran “sedimento” o ruido.
Gráfico de Sedimentación (Scree Plot)
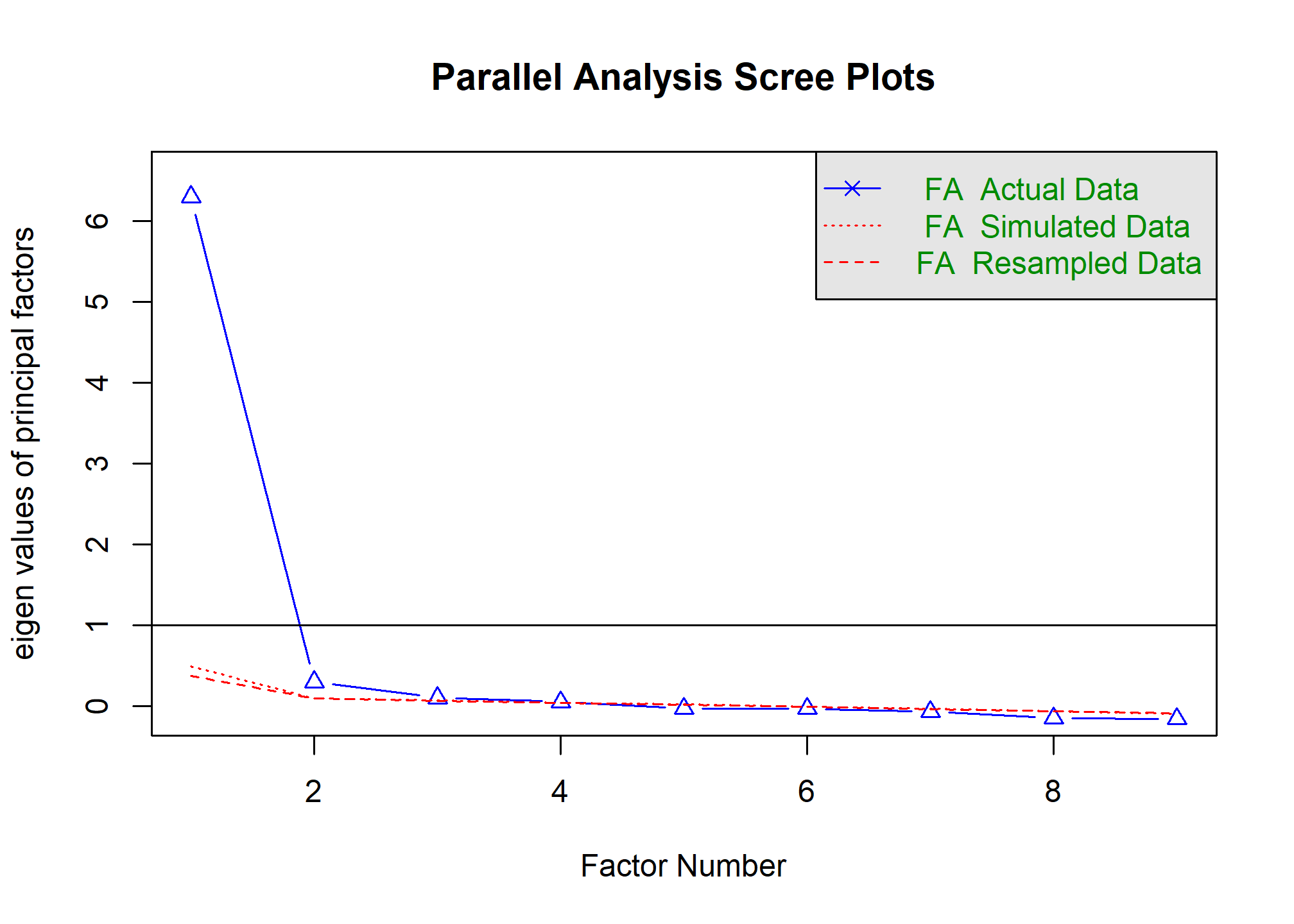 Ejemplo de Scree Plot: El “codo” parece estar después del 2do o 3er factor.
Ejemplo de Scree Plot: El “codo” parece estar después del 2do o 3er factor.
Ventaja: Intuitivo. Desventaja: A veces es ambiguo dónde está el “codo” (puede haber varios o ninguno claro).
Análisis Paralelo
Considerado uno de los métodos más robustos y precisos.
- Se generan múltiples conjuntos de datos aleatorios con el mismo número de variables y casos que los datos reales.
- Se realiza un ACP (o AFE) sobre cada conjunto de datos aleatorios y se calculan sus autovalores.
- Se promedian los autovalores obtenidos de los datos aleatorios para cada factor (o se usa el percentil 95).
- Regla: Se retienen los factores de los datos reales cuyos autovalores sean mayores que los autovalores correspondientes (promedio o percentil 95) generados por los datos aleatorios.
- La idea es retener solo factores que expliquen más varianza de lo que se esperaría por simple azar.
Ventaja: Más objetivo y menos propenso a sobre/subestimación que Kaiser o Scree Plot solo. Desventaja: Más complejo de calcular manualmente (pero fácil con software).
3. Métodos de Extracción de Factores
Una vez decidido el número de factores, se elige un método para “extraerlos” (estimar las cargas factoriales).
- Métodos de Factor Común (buscan explicar la covarianza/correlación):
- Ejes Principales (Principal Axis Factoring - PAF) / Mínimos Cuadrados Ordinarios (OLS o ULS - Unweighted Least Squares):
- No asume normalidad multivariante.
- Busca minimizar la diferencia entre las correlaciones observadas y las reproducidas por el modelo factorial.
fa()en R confm="minres"(Mínimos Cuadrados Residuales, por defecto),fm="pa"(Ejes Principales),fm="uls"son opciones robustas.
- Ejes Principales (Principal Axis Factoring - PAF) / Mínimos Cuadrados Ordinarios (OLS o ULS - Unweighted Least Squares):
3. Métodos de Extracción de Factores
- Métodos de Factor Común (buscan explicar la covarianza/correlación):
- Máxima Verosimilitud (Maximum Likelihood - ML):
- Asume normalidad multivariante.
- Estima cargas factoriales que maximizan la probabilidad de observar la matriz de correlaciones muestral.
- Ventaja: Permite calcular tests de bondad de ajuste e intervalos de confianza para las cargas (inferencia).
- Si no hay normalidad, los SE y tests pueden ser incorrectos.
- Otros: Mínimos Cuadrados Generalizados (GLS), Alfa Factoring, Imagen Factoring.
- Máxima Verosimilitud (Maximum Likelihood - ML):
4. Rotación Factorial: Hacia la Simplicidad
La solución factorial inicial (matriz de cargas sin rotar) a menudo es difícil de interpretar:
* Muchas variables pueden tener cargas moderadas en múltiples factores.
* Es difícil ver qué variables definen claramente cada factor.
Objetivo de la Rotación: Transformar matemáticamente los ejes de los factores en el espacio multidimensional para obtener una estructura más simple e interpretable, donde:
* Cada variable cargue alto en un solo factor (o muy pocos).
* Cada variable cargue bajo (cercano a cero) en los demás factores.
* Cada factor esté definido por un conjunto claro de variables.
Importante: La rotación no cambia la cantidad total de varianza explicada por la solución factorial ni las comunalidades de las variables. Solo redistribuye la varianza entre los factores rotados.
Tipos de Rotación Factorial
La elección depende de si teóricamente esperamos que los factores latentes estén o no correlacionados entre sí.
- Rotación Ortogonal (Factores NO Correlacionados):
- Los ejes de los factores se rotan manteniendo un ángulo de 90° entre ellos. Los factores resultantes son independientes (correlación cero).
- Método más común: VARIMAX. Busca maximizar la varianza de las cargas dentro de cada factor (simplifica las columnas de la matriz factorial). Tiende a producir factores con pocas cargas muy altas y muchas cercanas a cero.
- Otros: QUARTIMAX (simplifica filas), EQUAMAX (compromiso).
- Cuándo usar: Si se asume que los constructos latentes son conceptualmente distintos e independientes.
Tipos de Rotación Factorial
- Rotación Oblicua (Factores SÍ Correlacionados):
- Los ejes pueden rotar con ángulos distintos a 90°. Los factores resultantes pueden estar correlacionados.
- Métodos comunes: PROMAX, OBLIMIN DIRECTO.
- Cuándo usar: Si es teóricamente plausible que los factores latentes estén relacionados (muy común en ciencias sociales). Ej: Ansiedad y Depresión.
- Produce dos matrices: Matriz de Patrón (cargas directas, como coeficientes de regresión) y Matriz de Estructura (correlaciones variable-factor). La de Patrón suele ser la principal para interpretar.
- También entrega la matriz de correlación entre factores.
Recomendación: A menudo es bueno probar ambas y ver cuál da la solución más interpretable y teóricamente coherente. Si la correlación entre factores en una rotación oblicua es muy baja (ej. < |0.2| o |0.3|), la solución ortogonal puede ser preferible.
Interpretación de la Matriz Factorial
La Matriz de Cargas Factoriales
Después de la extracción (y usualmente rotación), obtenemos la matriz de cargas factoriales.
* Filas: Variables observadas (ítems).
* Columnas: Factores latentes extraídos.
* Celdas (\(\lambda_{ij}\)): La carga factorial de la variable \(i\) en el factor \(j\).
Interpretación de una Carga Factorial (\(\lambda_{ij}\)):
* Indica la fuerza y dirección de la relación lineal entre la variable observada \(X_i\) y el factor latente \(F_j\).
* Si la matriz es de correlaciones (variables estandarizadas), \(\lambda_{ij}\) es la correlación entre el ítem y el factor.
* \((\lambda_{ij})^2\): Es la proporción de varianza de la variable \(X_i\) que es explicada por el factor \(F_j\).
La Matriz de Cargas Factoriales
Ejemplo (Matriz NO Rotada): Podría ser confusa.
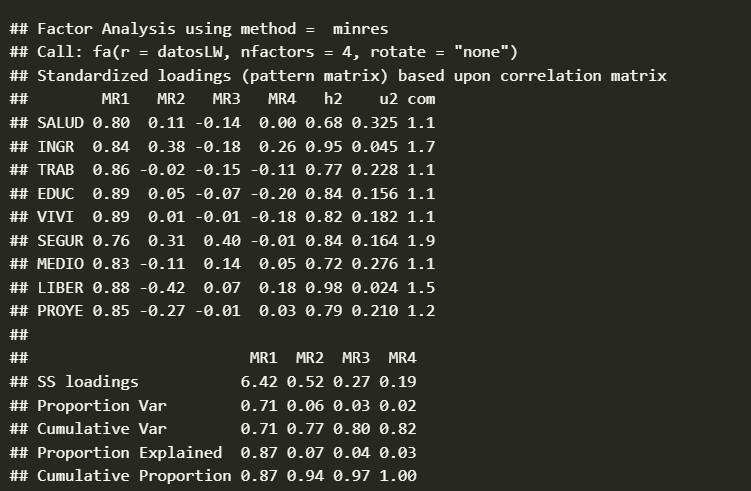
Interpretando la Matriz Factorial (Post-Rotación)
El objetivo es lograr una “Estructura Simple”:
- Identificar Cargas Significativas:
- No hay un corte universal, pero comúnmente se consideran “salientes” o “significativas” cargas con valor absoluto:
- > 0.30 o 0.32 (explica ~10% de la varianza del ítem).
- > 0.40 (más aceptable).
- > 0.50 (bueno).
- > 0.70 (excelente, explica ~50% de la varianza del ítem).
- No hay un corte universal, pero comúnmente se consideran “salientes” o “significativas” cargas con valor absoluto:
Interpretando la Matriz Factorial (Post-Rotación)
- Asignar Ítems a Factores:
- Idealmente, cada ítem debe tener una carga alta en UN SOLO factor y cargas bajas (<0.30 aprox.) en los demás.
- Si un ítem carga alto en múltiples factores (carga cruzada), es problemático para la interpretación. Podría ser un ítem complejo o mal redactado. Considerar eliminarlo o revisar la teoría.
- Nombrar los Factores:
- Una vez identificados los ítems que “pertenecen” a cada factor (los que cargan alto en él), se busca el hilo conceptual común entre esos ítems.
- El nombre del factor debe reflejar ese concepto subyacente de la manera más precisa y concisa posible. Es un acto de interpretación teórica.
Ejemplo de Matriz Rotada
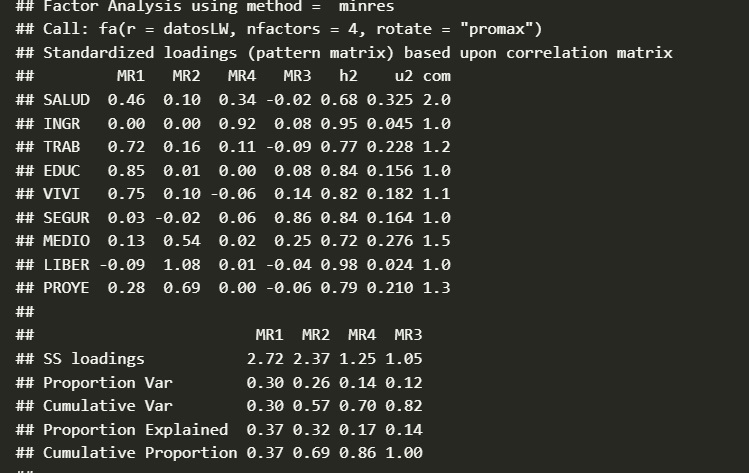
Ejemplo de Matriz Rotada
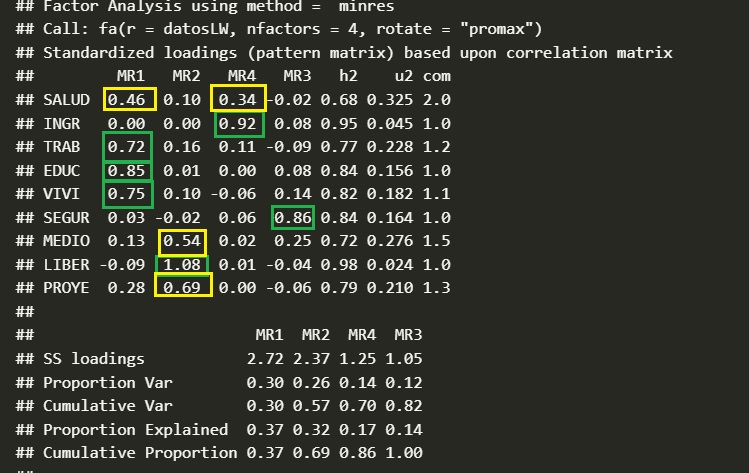
La Evaluación del Modelo Factorial
Criterios para Evaluar la Solución Factorial
Una vez obtenida una solución factorial (número de factores, cargas), ¿cómo sabemos si es “buena”?
- Interpretabilidad Teórica: ¿Tienen sentido los factores? ¿Son consistentes con la teoría o investigaciones previas? ¿Los ítems que cargan juntos son conceptualmente coherentes? ¡Esto es primordial!
- Estructura Simple: ¿Cada variable carga alto en un solo factor? ¿Pocas cargas cruzadas?
Criterios para Evaluar la Solución Factorial
- Comunalidades (\(h^2\)):
- Proporción de la varianza de cada variable explicada por el conjunto de factores retenidos.
- Se busca que sean razonablemente altas (ej. > 0.3, idealmente > 0.5). Comunalidades muy bajas indican que el ítem no es bien explicado por la solución factorial (podría no pertenecer a ninguno de los constructos).
- Varianza Explicada por Cada Factor y Total:
- ¿Cuánta varianza de las variables originales explica cada factor?
- ¿Cuánta varianza total explican todos los factores juntos? (Se busca un % razonable, ej. > 50-60%).
- Índices de Bondad de Ajuste (si se usó ML o GLS para extracción):
- Evalúan qué tan bien la matriz de correlaciones reproducida por el modelo factorial se ajusta a la matriz de correlaciones observada.
Estadísticos de Ajuste Comunes (Principalmente para ML)
- Chi-cuadrado (\(\chi^2\)) del Modelo:
- \(H_0\): El modelo de k factores se ajusta perfectamente a los datos poblacionales.
- Resultado deseado: Un \(\chi^2\) NO significativo (p > 0.05).
- Problema: Muy sensible al tamaño muestral (con N grande, casi siempre es significativo, incluso para modelos buenos).
- RMSR (Root Mean Square of Residuals) o SRMR (Standardized RMR):
- Media de las diferencias (residuos) entre las correlaciones observadas y las reproducidas.
- Valores más cercanos a 0 indican mejor ajuste. SRMR < 0.08 o < 0.05 es bueno.
Estadísticos de Ajuste Comunes (Principalmente para ML)
- RMSEA (Root Mean Square Error of Approximation):
- Mide el error de aproximación por grado de libertad, penaliza complejidad.
- < 0.05: Buen ajuste.
- 0.05 - 0.08: Ajuste aceptable/razonable.
- 0.08 - 0.10: Ajuste mediocre.
- > 0.10: Mal ajuste. (Idealmente con IC 90% que no supere 0.08 o 0.10).
- TLI (Tucker-Lewis Index) / CFI (Comparative Fit Index):
- Índices de ajuste incremental, comparan con un modelo nulo (independencia).
- Valores > 0.90 aceptable, > 0.95 bueno.
- BIC (Bayesian Information Criterion) / AIC (Akaike Information Criterion):
- Para comparar modelos no anidados. Valores más bajos indican mejor ajuste relativo, penalizando por complejidad.
(Estos índices son más centrales en AFC, pero se reportan en AFE con ML).
Cálculo y Uso de Puntuaciones Factoriales
¿Qué son las Puntuaciones Factoriales?
Una vez validada la estructura factorial, a menudo queremos asignar a cada individuo un puntaje que represente su nivel en cada uno de los factores latentes identificados.
- Estas son estimaciones del valor que cada individuo tendría en la variable latente (no observable).
- Existen varios métodos para calcularlas (Regresión, Bartlett, Anderson-Rubin). El método por defecto en
psych::fa()es “Thurstone” (basado en regresión). - Las puntuaciones factoriales suelen estar estandarizadas (media 0, DE aprox. 1 si los factores son ortogonales).
Uso de las Puntuaciones Factoriales
Las puntuaciones factoriales convierten los factores latentes en “variables” que podemos usar en análisis posteriores:
- Reducción de Datos: En lugar de trabajar con (ej.) 20 ítems, trabajamos con 2 o 3 puntuaciones factoriales que resumen la información clave.
- Como Variables en Otros Modelos:
- Variables Independientes: Predecir una VD usando las puntuaciones factoriales (ej. ¿Cómo las “Oportunidades Materiales” afectan la “Satisfacción Vital”?).
- Variables Dependientes: ¿Qué características sociodemográficas predicen el nivel de “Autoritarismo” (puntuación factorial)?
Uso de las Puntuaciones Factoriales
- Análisis de Perfiles o Clusters: Agrupar individuos según sus perfiles de puntuaciones en los diferentes factores.
- Comparaciones de Grupos: Usar pruebas t o ANOVA para ver si diferentes grupos (ej. hombres vs mujeres) difieren en sus puntuaciones factoriales promedio.
Precaución: Recordar que son estimaciones de los factores latentes, no los factores en sí. Tienen un grado de indeterminación.
Próximos Pasos
En el práctico:
- Aplicaremos los criterios para decidir el número de factores (Kaiser, Scree Plot, Análisis Paralelo).
- Extraeremos factores usando un método apropiado.
- Realizaremos rotaciones (Varimax y Promax).
- Interpretaremos las matrices factoriales rotadas y nombraremos los factores.
- Calcularemos y guardaremos las puntuaciones factoriales.
